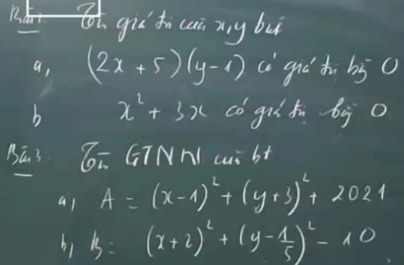Bài 3:
a: \(A=\left(x-1\right)^2+\left(y+3\right)^2+2021\ge2021\forall x,y\)
Dấu '=' xảy ra khi x=1 và y=-3
b: \(B=\left(x+2\right)^2+\left(y-\dfrac{1}{5}\right)^2-10\ge-10\forall x,y\)
Dấu '=' xảy ra khi x=-2 và y=1/5
Bài 1:
\(a,\left(2x+5\right)\left(y-1\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}2x+5=0\\y-1=0\end{matrix}\right.\\
\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{2}\\y=1\end{matrix}\right.\\
n,x^2+3x=0\\
\Leftrightarrow x\left(x+3\right)=0\\
\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\end{matrix}\right.\)
Bài 2:
a, Ta có:\(A=\left(x-1\right)^2+\left(y+3\right)^2+2021\ge2021\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
Vậy \(A_{min}=2021\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-3\end{matrix}\right.\)
b, Ta có: \(B=\left(x+2\right)^2+\left(y-\dfrac{1}{5}\right)^2-10\ge-10\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{5}\end{matrix}\right.\)Vậy \(B_{min}=-10\Leftrightarrow\left\{{}\begin{matrix}x=-2\\y=\dfrac{1}{5}\end{matrix}\right.\)