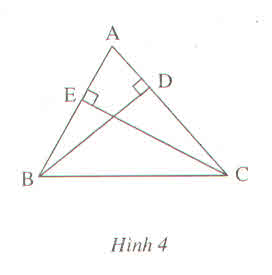
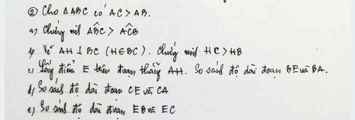a: Xét ΔABC có AC>AB
mà góc đối diện với cạnh AC là góc ABC
và góc đối diện với cạnh AB là góc ACB
nên \(\widehat{ABC}>\widehat{ACB}\)
b: Xét ΔABC có AC>AB
mà hình chiếu của AC trên BC là HC
và hình chiếu của AB trên BC là HB
nên HC>HB
c: Ta có: ΔBHE vuông tại H
nên \(\widehat{BEH}< 90^0\)
\(\Leftrightarrow180^0-\widehat{BEH}>90^0\)
\(\Leftrightarrow\widehat{BEA}>90^0\)
Xét ΔBEA có góc BEA tù
mà BA là cạnh đối diện với góc BEA
nên BA là cạnh lớn nhất trong ΔBEA
=>BA>BE
d:
Ta có: ΔCHE vuông tại H
nên \(\widehat{CEH}< 90^0\)
\(\Leftrightarrow180^0-\widehat{CEH}>90^0\)
\(\Leftrightarrow\widehat{CEA}>90^0\)
Xét ΔCEA có góc CEA tù
mà CA là cạnh đối diện với góc CEA
nên CA là cạnh lớn nhất trong ΔCEA
=>CA>CE
e: Xét ΔEBC có HB<HC
mà HB là hình chiếu của EB trên BC
và HC là hình chiếu của EC trên BC
nên EB<EC