Ta có: \(x^2\ge0\forall x\in R\)
Suy ra cặp thứ 3 sẽ thỏa mãn điều kiện của đề bài
Đúng 0
Bình luận (0)
§2. Bất phương trình và hệ bất phương trình một ẩn
Các câu hỏi tương tự
1. giải bpt
a) |x2-5x-9||x-6|
b) frac{text{-3}}{text{|x-2|-3}}≥|x-2|+1
2. tìm m để pt (m+1)x2-2(m-1)X+3m-3≥0 vô nghiệm
3. tìm m để pt (m+1)x2-2(m-1)x+2m+10 có 2 nghiệm x1,x2 thỏa: x11x2
4. Tìm txđ hàm số ysqrt{text{|x^2+3x-4|-x+8}}
Giải giúp em với Em cảm ơn nhiều 💚
Đọc tiếp
1. giải bpt
a) |x2-5x-9|<|x-6|
b) \(\frac{\text{-3}}{\text{|x-2|-3}}\)≥|x-2|+1
2. tìm m để pt (m+1)x2-2(m-1)X+3m-3≥0 vô nghiệm
3. tìm m để pt (m+1)x2-2(m-1)x+2m+1=0 có 2 nghiệm x1,x2 thỏa: x1<1<x2
4. Tìm txđ hàm số y=\(\sqrt{\text{|x^2+3x-4|-x+8}}\)
Giải giúp em với> Em cảm ơn nhiều 💚
Tìm m để \(x\in\) [ \(0;+\infty\)) đều là nghiệm của bất phương trình \(\left(m^2-1\right)x^2-8mx+9-m^2\ge0\)
1. Cho phương trình x2 - 6x + m = 0.
a) Với giá trị nào của m thì phương trình có 2 nghiệm trái dấu.
b) Tìm m để phương trình có 2 nghiệm x1,x2 thỏa mãn điều kiện x1 - x2 = 4.
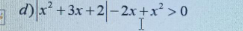Giải bpt sau :
tìm m để hệ pt có nghiệm
\(\left\{{}\begin{matrix}\sqrt{1+x}+\sqrt{y-2}=\sqrt{m}\\\sqrt{1+y}+\sqrt{x-2}=\sqrt{m}\end{matrix}\right.\)
Giải và biện luận bất phương trình theo tham số m:
a) m(x - m) \(\le\) x - 1
b) mx + 6 > 2x + 3m
c) (m + 1)x + m < 3x+4
Viết điều kiện của mỗi bất phương trình sau :
a) \(2x-3-\dfrac{1}{x-5}< x^2-x\)
b) \(x^3\le1\)
c) \(\sqrt{x^2-x-2}< \dfrac{1}{2}\)
d) \(\sqrt[3]{x^4+x-1}+x^2-1\ge0\)