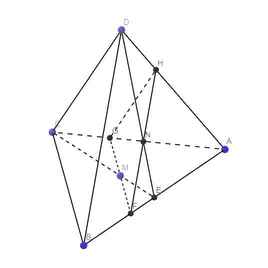
Gọi E là trung điểm AB
Do M là trọng tâm ABC \(\Rightarrow\dfrac{ME}{CE}=\dfrac{1}{3}\)
Do N là trọng tâm ABD \(\Rightarrow\dfrac{NE}{DE}=\dfrac{1}{3}\)
\(\Rightarrow\dfrac{ME}{CE}=\dfrac{NE}{DE}\Rightarrow MN||CD\) (Talet đảo)
Mà \(CD\in\left(BCD\right)\Rightarrow MN||\left(BCD\right)\)
b.
Trong mp (ABC), qua M kẻ đường thẳng song song BC cắt AB tại F và AC tại G
Trong mp (ABD), nối FN kéo dài cắt AD tại H
\(\Rightarrow\) Tam giác FGH là thiết diện của (P) và tứ diện
Đúng 2
Bình luận (0)
