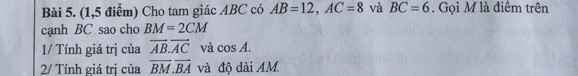\(BM=2CM=2\left(BC-BM\right)\Rightarrow3BM=2BC\Rightarrow BM=\dfrac{2}{3}BC=4\)
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2AB.AC}=\dfrac{43}{48}\)
\(\overrightarrow{AB}.\overrightarrow{AC}=AB.AC.cosA=86\)
\(cosB=\dfrac{AB^2+BC^2-AC^2}{2AB.BC}=\dfrac{29}{36}\)
\(\overrightarrow{BM}.\overrightarrow{BA}=BM.AB.cosB=\dfrac{116}{3}\)
\(AM=\sqrt{AB^2+BM^2-2AB.BM.cosB}=\dfrac{2\sqrt{186}}{3}\)
Oxy , A(1;2) ; B(2;5) , đường d x-2y-2=0.Tìm tọa độ M\(\in\)d sao cho
a)\(\left|\overrightarrow{MA}+\overrightarrow{MB}\right|\) đạt giá trị nhỏ nhất
b)\(MA^2+MB^2\) đạt giá trị nhỏ nhất
Oxy , A(1;2) ; B(2;5) , đường d x-2y-2=0.Tìm tọa độ M\(∈\)d sao cho
a) \(\left|\overrightarrow{MA}+3\overrightarrow{MB}\right|\) đạt giá trị nhỏ nhất
b) Giá trị tuyệt đối của MA-MB đạt giá trị lớn nhất
Cho hình bình hành ABCD. Gọi N là trung điểm cạnh CD. Trên cạnh AC lấy điểm M sao cho AM = 2MC; Phân tích các vec tơ sau theo hai véc tơ ABvà AD
a. vecto ac
b) vecto AM
c) vecto an
Giúp mik lm bài 2 3 4 5 vs ạ
Cho AB=a, I là trung điểm của AB.Tìm M sao cho 2AM^2+BM^2=a^2
Cho hình chữ nhật ABCD. Gọi E là hình chiếu cuarB trên AC, F và G là trung điểm của AE và CD. Chứng minh BF vuông góc với FG
cho tam giác ABC gọi K là điểm xác định bởi ( 2vectoKA+3vectoKB+vectoKC=vecto0) .gọi M,N là hai điểm phân biệt thõa mãn ( vectoMN= 2vectoMA+3vectoMB+vectoMC) chứng minh M,N luôn đi qua một điểm có định
Cho tam giác ABC, D là điểm thuộc cạnh BC sao cho DC= 2DB. Nếu \(\overrightarrow{AD}=m\overrightarrow{AB}+n\overrightarrow{AC}\) thì m và n bằng bao nhiêu?
Cho hình thang vuông ABCD,đường cao AB=2a,đáy lớn BC=3a
a) tính \(\overrightarrow{AB}\).\(\overrightarrow{CD}\)
\(\overrightarrow{BD}.\overrightarrow{BC}\)
\(\overrightarrow{AC}.\overrightarrow{BD}\)
b)gọi I là trung điểm của CD tính \(\overrightarrow{AI.}\overrightarrow{BD}\)và suy ra góc của 2 vecto AI và BD
cho tam giác ABC cân tại A=2a cmr Sin2a=2SinaCosa
