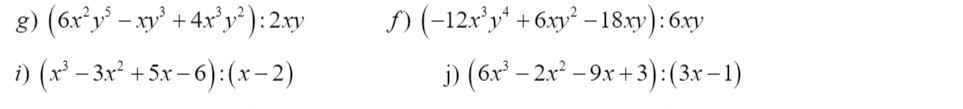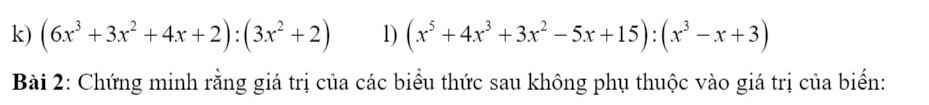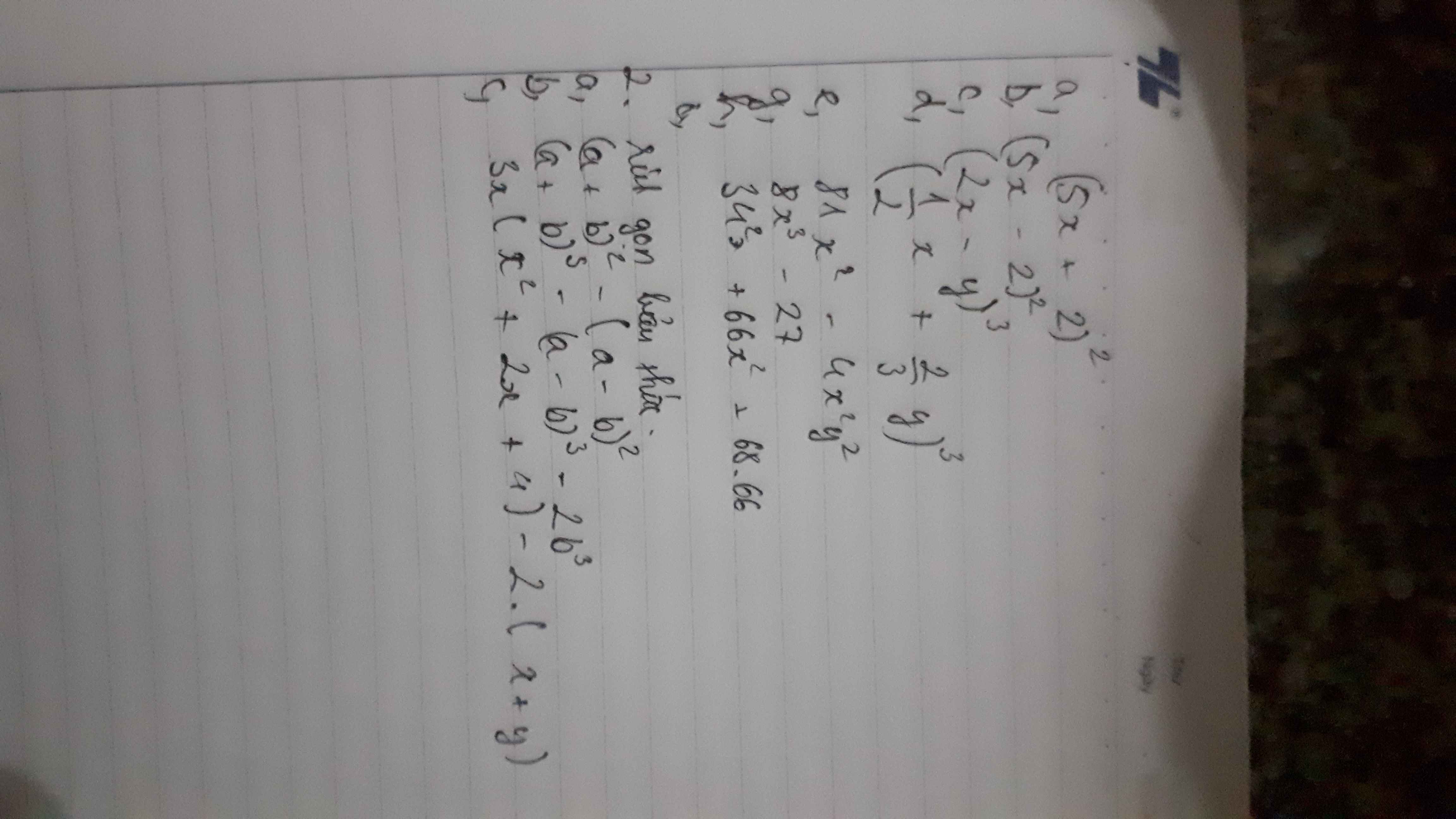\(g,=3xy^4-\dfrac{1}{2}y^2+2x^2y\\ f,=-2x^2y^3+y-3\\ i,=\left(x^3-2x^2-x^2+2x+3x-6\right):\left(x-2\right)\\ =\left(x-2\right)\left(x^2-x+3\right):\left(x-2\right)\\ =x^2-x+3\\ j,=\left[2x^2\left(3x-1\right)-3\left(3x-1\right)\right]:\left(3x-1\right)\\ =2x^2-3\\ k,=\left[2x\left(3x^2+2\right)+\left(3x^2+2\right)\right]:\left(3x^2+2\right)\\ =2x+1\\ l,=\left(x^5-x^3+3x^2+5x^3-5x+15\right):\left(x^3-x+3\right)\\ =\left[x^2\left(x^3-x+3\right)+5\left(x^3-x+3\right)\right]:\left(x^3-x+3\right)\\ =x^2+5\)
g,=3xy4−12y2+2x2y
f,=−2x2y3+y−3
i,=(x3−2x2−x2+2x+3x−6):(x−2)=(x−2)(x2−x+3):(x−2)=x2−x+3
j,=[2x2(3x−1)−3(3x−1)]:(3x−1)=2x2−3
k,=[2x(3x2+2)+(3x2+2)]:(3x2+2)=2x+1
l,=(x5−x3+3x2+5x3−5x+15):(x3−x+3)=[x2(x3−x+3)+5(x3−x+3)]:(x3−x+3)=x2+5