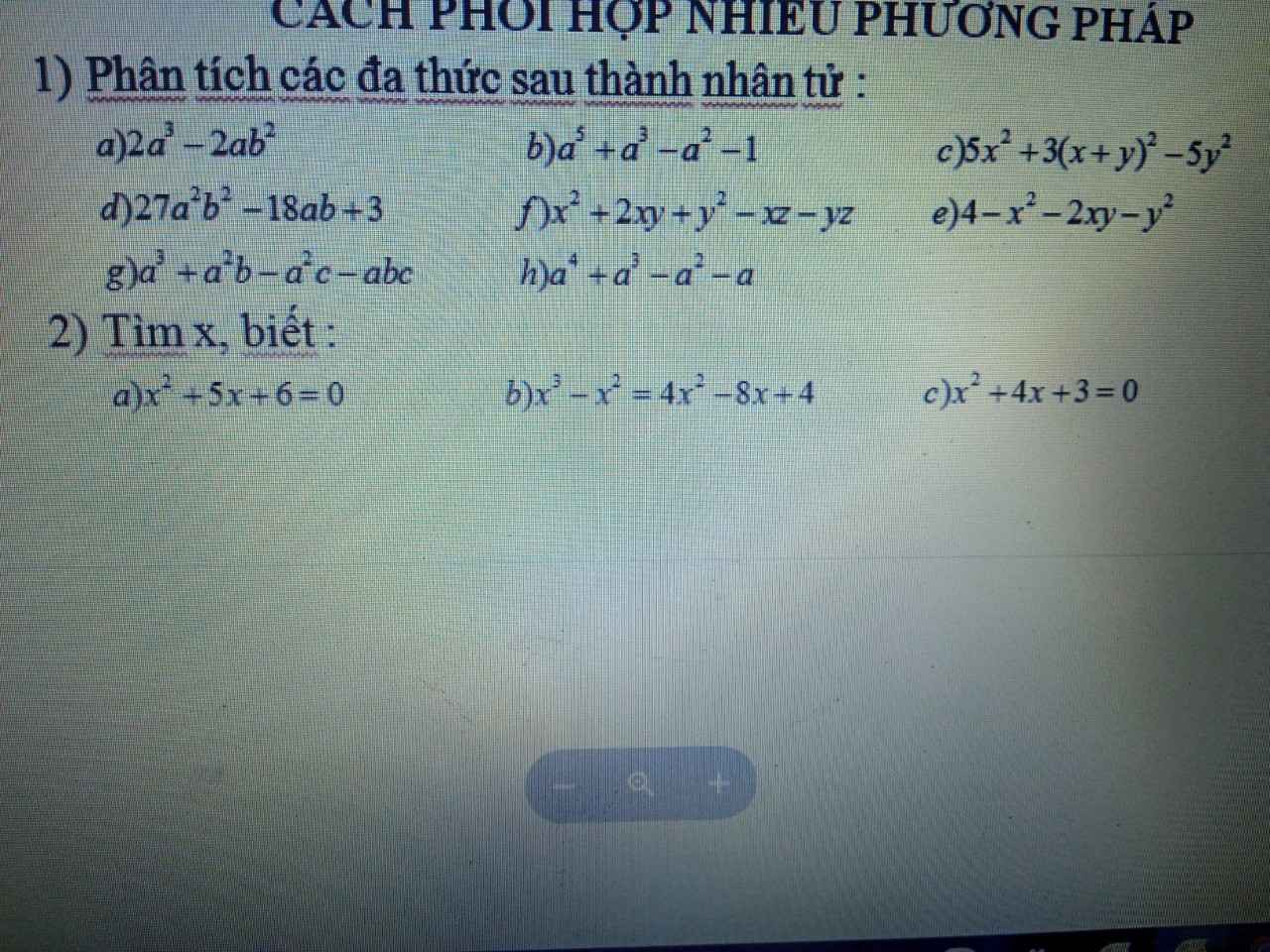
\(1,\\ a,=2a\left(a^2-b^2\right)=2a\left(a-b\right)\left(a+b\right)\\ b,=a^2\left(a^3-1\right)+\left(a^3-1\right)\\ =\left(a^2+1\right)\left(a^3-1\right)=\left(a^2+1\right)\left(a-1\right)\left(a^2+a+1\right)\\ c,=5\left(x-y\right)\left(x+y\right)+3\left(x+y\right)^2\\ =\left(x+y\right)\left(5x-5y+3x+3y\right)\\ =\left(x+y\right)\left(8x-2y\right)=2\left(4x-y\right)\left(x+y\right)\\ d,=3\left(9a^2b^2-6ab+1\right)=3\left(3ab-1\right)^2\\ f,=\left(x+y\right)^2-z\left(x+y\right)=\left(x+y\right)\left(x+y-z\right)\\ e,=\left(2-x-y\right)\left(2+x+y\right)\\ g,=a^2\left(a+b\right)-ac\left(a+b\right)=a\left(a-c\right)\left(a+b\right)\\ h,=a^2\left(a^2-1\right)-a\left(a^2-1\right)\\ =a\left(a-1\right)^2\left(a+1\right)\)
\(2,\\ a,\Leftrightarrow\left(x+2\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-3\end{matrix}\right.\\ b,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\\ c,\Leftrightarrow\left(x+1\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-3\end{matrix}\right.\)