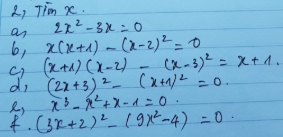\(a,A=\left(x+y-3x\right)\left(x+y+3x\right)=\left(y-2x\right)\left(4x+y\right)\\ b,A=9-\left(x^2+2xy+y^2\right)=9-\left(x+y\right)^2=\left(9-x-y\right)\left(9+x+y\right)\)
\(a,A=\left(x+y\right)^2-9x^2=\left(x+y\right)^2-\left(3x\right)^2=\left(x+y-3x\right).\left(x+y+3x\right)=\left(y-2x\right).\left(4x+y\right)\) \(b,A=9-x^2-2xy-y^2=3^2-\left(x^2+2xy+y^2\right)=3^2-\left(x+y\right)^2=\left(3-x-y\right).\left(3+x+y\right)\)
\(A=\left(x+y-3x\right)\left(x+y+3x\right)=\left(y-2x\right)\left(y+4x\right)\)
\(A=9-\left(x^2+2xy+y^2\right)=9-\left(x+y\right)^2=\left(3-x-y\right)\left(3+x+y\right)\)
Không làm tắt
Ko làm tắt
