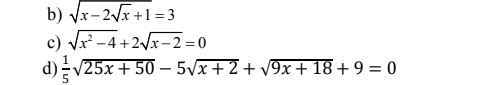b)\(\sqrt{x-2\sqrt{x}+1}=3\left(đk:x\ge0\right)\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x}-1\right)^2}=3\)
\(\Leftrightarrow\left|\sqrt{x}-1\right|=3\)
\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=3\\\sqrt{x}-1=-3\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}=4\\\sqrt{x}=-2\left(VLý\right)\end{matrix}\right.\)\(\Leftrightarrow x=16\left(tm\right)\)
c) \(\sqrt{x^2-4}+2\sqrt{x-2}=0\left(đk:x\ge2\right)\)
\(\Leftrightarrow\sqrt{\left(x-2\right)\left(x+2\right)}+2\sqrt{x-2}=0\)
\(\Leftrightarrow\sqrt{x-2}\left(\sqrt{x+2}+2\right)=0\)
\(\Leftrightarrow\sqrt{x-2}=0\)(do \(\sqrt{x+2}+2\ge2>0\))
\(\Leftrightarrow x-2=0\Leftrightarrow x=2\left(tm\right)\)
d) \(đk:x\ge-2\)
\(pt\Leftrightarrow\sqrt{x+2}-5\sqrt{x+2}+3\sqrt{x+2}=-9\)
\(\Leftrightarrow-\sqrt{x+2}=-9\Leftrightarrow\sqrt{x+2}=9\)
\(\Leftrightarrow x+2=81\Leftrightarrow x=79\left(tm\right)\)
c: Ta có: \(\sqrt{x^2-4}+2\sqrt{x-2}=0\)
\(\Leftrightarrow x-2=0\)
hay x=2
d: Ta có: \(\dfrac{1}{5}\sqrt{25x+50}-5\sqrt{x+2}+\sqrt{9x+18}+9=0\)
\(\Leftrightarrow\sqrt{x+2}-5\sqrt{x+2}+3\sqrt{x+2}=-9\)
\(\Leftrightarrow x+2=81\)
hay x=79