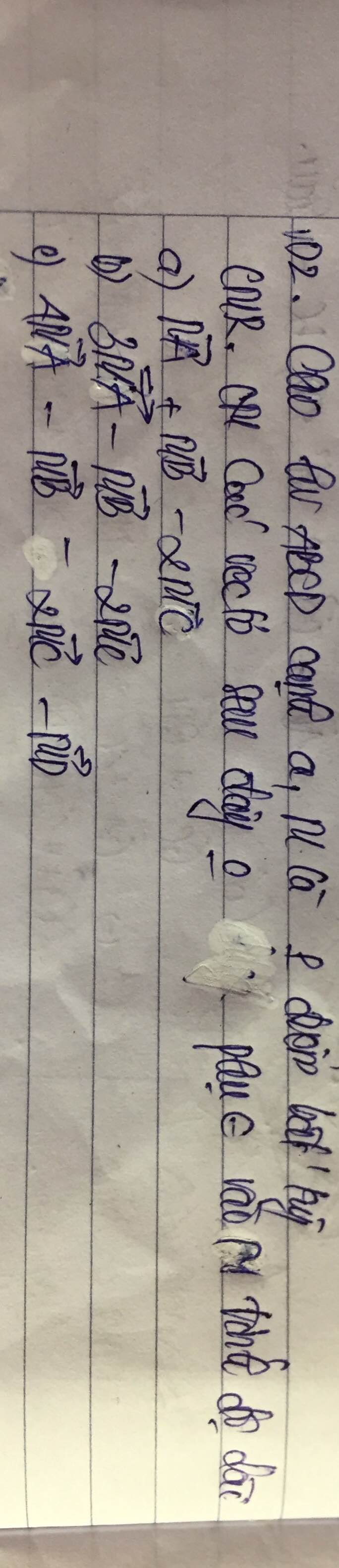a.
\(\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}=\overrightarrow{MA}+\overrightarrow{MB}+2\overrightarrow{CM}=\left(\overrightarrow{CM}+\overrightarrow{MA}\right)+\left(\overrightarrow{CM}+\overrightarrow{MB}\right)\)
\(=\overrightarrow{CA}+\overrightarrow{CB}\) không phụ thuộc M
Gọi E là trung điểm AB \(\Rightarrow\overrightarrow{CA}+\overrightarrow{CB}=2\overrightarrow{CE}\)
\(\Rightarrow\left|\overrightarrow{MA}+\overrightarrow{MB}-2\overrightarrow{MC}\right|=2\left|\overrightarrow{CE}\right|=2\sqrt{BC^2+BE^2}=2\sqrt{BC^2+\left(\dfrac{AB}{2}\right)^2}=a\sqrt{5}\)
b.
\(3\overrightarrow{MA}-\overrightarrow{MB}-2\overrightarrow{MC}=3\overrightarrow{MA}+\overrightarrow{BM}+2\overrightarrow{CM}=\left(\overrightarrow{BM}+\overrightarrow{MA}\right)+2\left(\overrightarrow{CM}+\overrightarrow{MA}\right)\)
\(=\overrightarrow{BA}+2\overrightarrow{CA}\) không phụ thuộc M
Đặt \(\overrightarrow{u}=\overrightarrow{BA}+2\overrightarrow{CA}=\overrightarrow{BA}+2\left(\overrightarrow{CB}+\overrightarrow{CD}\right)=3\overrightarrow{CD}+2\overrightarrow{CB}\)
\(\Rightarrow\left|\overrightarrow{u}\right|^2=9CD^2+4CB^2+12\overrightarrow{CD}.\overrightarrow{CB}=9CD^2+4CB^2=13a^2\)
\(\Rightarrow\left|\overrightarrow{u}\right|=a\sqrt{13}\)
c.
Đặt \(\overrightarrow{v}=4\overrightarrow{MA}-\overrightarrow{MB}-2\overrightarrow{MC}-\overrightarrow{MD}\)
\(=4\overrightarrow{MA}+\overrightarrow{BM}+2\overrightarrow{CM}+\overrightarrow{DM}\)
\(=\left(\overrightarrow{BM}+\overrightarrow{MA}\right)+2\left(\overrightarrow{CM}+\overrightarrow{MA}\right)+\left(\overrightarrow{DM}+\overrightarrow{MA}\right)\)
\(=\overrightarrow{BA}+2\overrightarrow{CA}+\overrightarrow{DA}\)
\(=2\overrightarrow{CA}-\left(\overrightarrow{AB}+\overrightarrow{AD}\right)\)
\(=2\overrightarrow{CA}-\overrightarrow{AC}=2\overrightarrow{CA}+\overrightarrow{CA}\)
\(=3\overrightarrow{CA}\) không phụ thuộc M
\(\left|\overrightarrow{v}\right|=3\left|\overrightarrow{CA}\right|=3CA=3a\sqrt{2}\)