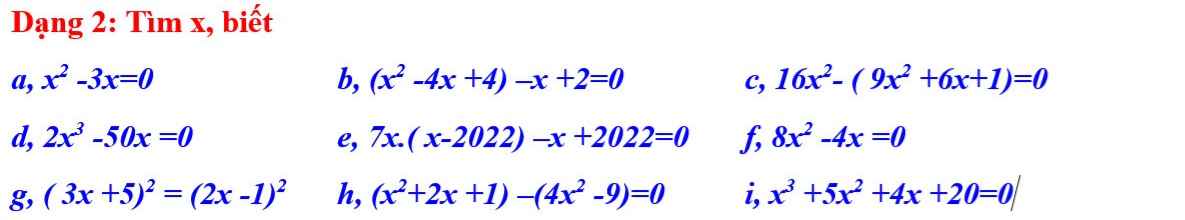a. x2 - 3x = 0
<=> x(x - 3) = 0
<=> \(\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\)
b. (x2 - 4x + 4) - x + 2 = 0
<=> (x - 2)2 - (x - 2) = 0
<=> (x - 2 - 1)(x - 2) = 0
<=> (x - 3)(x - 2) = 0
<=> \(\left[{}\begin{matrix}x-3=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)
c. 16x2 - (9x2 + 6x + 1) = 0
<=> 16x2 - (3x + 1)2 = 0
<=> (4x)2 - (3x + 1)2 = 0
<=> (4x - 3x - 1)(4x + 3x + 1) = 0
<=> (x - 1)(7x + 1) = 0
<=> \(\left[{}\begin{matrix}x-1=0\\7x+1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{-1}{7}\end{matrix}\right.\)
d. 2x3 - 50x = 0
<=> 2x(x2 - 25) = 0
<=> 2x(x - 5)(x + 5) = 0
<=> \(\left[{}\begin{matrix}2x=0\\x-5=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
e. 7x(x - 2022) - x + 2022 = 0
<=> 7x(x - 2022) - (x - 2022) = 0
<=> (7x - 1)(x - 2022) = 0
<=> \(\left[{}\begin{matrix}7x-1=0\\x-2022=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{7}\\x=2022\end{matrix}\right.\)
f. 8x2 - 4x = 0
<=> 4x(2x - 1) = 0
<=> \(\left[{}\begin{matrix}4x=0\\2x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\end{matrix}\right.\)
g. (3x + 5)2 = (2x - 1)2
<=> (3x + 5)2 - (2x - 1)2 = 0
<=> (3x + 5 - 2x + 1)(3x + 5 + 2x - 1) = 0
<=> (x + 6)(5x + 4) = 0
<=> \(\left[{}\begin{matrix}x+6=0\\5x+4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-6\\x=\dfrac{-4}{5}\end{matrix}\right.\)
h. (x2 + 2x + 1) - (4x2 - 9) = 0
<=> x2 + 2x + 1 - 4x2 + 9
<=> -3x2 + 2x + 10 = 0
<=> 3x2 - 2x - 10 = 0
<=> \(3x^2-2.\sqrt{3}.x.\dfrac{\sqrt{3}}{3}+\dfrac{1}{3}-\dfrac{31}{3}=0\)
<=> \(\left(\sqrt{3}x-\dfrac{\sqrt{3}}{3}\right)^2=\dfrac{31}{3}\)
<=> \(\left[{}\begin{matrix}\sqrt{3}x-\dfrac{\sqrt{3}}{3}=\dfrac{\sqrt{93}}{3}\\\sqrt{3}x-\dfrac{\sqrt{3}}{3}=\dfrac{-\sqrt{93}}{3}\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}\sqrt{3}x=\dfrac{\sqrt{93}+\sqrt{3}}{3}\\\sqrt{3}x=\dfrac{-\sqrt{93}+\sqrt{3}}{3}\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=\dfrac{1+\sqrt{31}}{3}\\x=\dfrac{1-\sqrt{31}}{3}\end{matrix}\right.\)
i. x3 + 5x2 + 4x + 20 = 0
<=> x2(x + 5) + 4(x + 5) = 0
<=> (x2 + 4)(x + 5) = 0
<=> \(\left[{}\begin{matrix}x^2+4=0\\x+5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2=-4\left(Vlí\right)\\x=-5\end{matrix}\right.\)