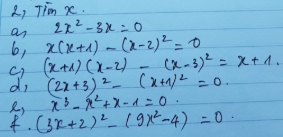\(a,=\left(x-y\right)\left(x+y\right)-2\left(x-y\right)=\left(x-y\right)\left(x+y-2\right)\\ b,=\left(2x-5\right)\left(2x+5\right)-\left(2x+7\right)\left(2x-5\right)\\ =\left(2x-5\right)\left(2x+5-2x-7\right)\\ =-2\left(2x-5\right)\\ c,=x^2\left(x+y\right)-4\left(x+y\right)=\left(x-2\right)\left(x+2\right)\left(x+y\right)\\ d,=0,25y\left(64x^3+z^3\right)=0,25y\left(4x+z\right)\left(16x^2-4xz+z^2\right)\\ e,=a^2+b^2+c^2+2ab+2ac+2bc+a^2+b^2+c^2+2ab-2bc-2ac-4c^2\\ =2a^2+2b^2-4c^2+4ab\\ =2\left(a+b\right)^2-4c^2=\left[\sqrt{2}\left(a+b\right)-2c\right]\left[\sqrt{2}\left(a+b\right)+2c\right]\)
\(f,=x^2\left(x^2-4x+4\right)=x^2\left(x-2\right)^2\\ g,=\left(2ab-a^2-b^2+c^2\right)\left(2ab+a^2+b^2-c^2\right)\\ =\left[c^2-\left(a-b\right)^2\right]\left[\left(a+b\right)^2-c^2\right]\\ =\left(c-a+b\right)\left(c+a-b\right)\left(a+b-c\right)\left(a+b+c\right)\\ h,=x^4y^4+4x^2y^2+4-4x^2y^2\\ =\left(x^2y^2+2\right)^2-\left(2xy\right)^2\\ =\left(x^2y^2+2xy+2\right)\left(x^2y^2-2xy+2\right)\\ k,=\left(x^2+y^2+z^2+2xy+2xz+2yz\right)-9y^2+12yz-4z^2\\ =\left(x+y+z\right)^2-\left(3y-2z\right)^2\\ =\left(x+y+z-3y+2z\right)\left(x+y+z+3y-2z\right)\\ =\left(x-2y+3z\right)\left(x+4y-z\right)\)
\(l,=\left(a-b+b-c\right)^3-3\left(a-b\right)\left(b-c\right)\left(a-b+b-c\right)+\left(c-a\right)^3\\ =\left(a-c\right)^3+\left(c-a\right)^3-3\left(a-b\right)\left(b-c\right)\left(a-c\right)\\ =\left(a-c+c-a\right)^3-3\left(a-c\right)\left(c-a\right)\left(a-c+c-a\right)-3\left(a-b\right)\left(b-c\right)\left(a-c\right)\\ =0^3-0-3\left(a-b\right)\left(b-c\right)\left(a-c\right)=-3\left(a-b\right)\left(b-c\right)\left(a-c\right)\)












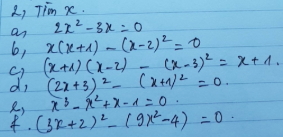 Không làm tắt
Không làm tắt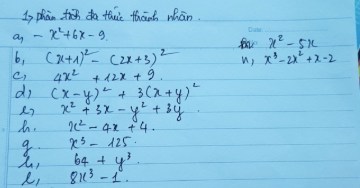 Ko làm tắt
Ko làm tắt