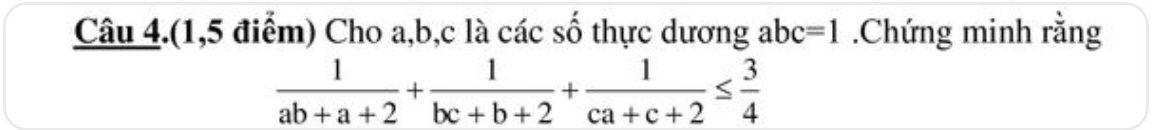Đẳng thức quen thuộc khi \(abc=1\)
\(\dfrac{1}{ab+a+1}+\dfrac{1}{bc+b+1}+\dfrac{1}{ca+c+1}=1\)
Chứng minh:
\(\dfrac{1}{ab+a+1}+\dfrac{1}{bc+b+1}+\dfrac{1}{ca+c+1}=\dfrac{1}{ab+a+1}+\dfrac{a}{abc+ab+a}+\dfrac{ab}{a.abc+abc+ab}\)
\(=\dfrac{1}{ab+a+1}+\dfrac{a}{1+ab+a}+\dfrac{ab}{a+1+ab}=\dfrac{1+a+ab}{ab+a+1}=1\)
Do đó:
\(VT=\dfrac{1}{ab+a+1+1}+\dfrac{1}{bc+b+1+1}+\dfrac{1}{ca+c+1+1}\)
\(VT\le\dfrac{1}{16}\left(\dfrac{9}{ab+a+1}+\dfrac{1}{1}+\dfrac{9}{bc+b+1}+\dfrac{1}{1}+\dfrac{9}{ca+c+1}+\dfrac{1}{1}\right)=\dfrac{12}{16}=\dfrac{3}{4}\) (đpcm)
\(\dfrac{1}{ab+a+2}=\dfrac{1}{ab+1+a+1}\le\dfrac{1}{4}\left(\dfrac{1}{ab+1}+\dfrac{1}{a+1}\right)\\ =\dfrac{1}{4}\left(\dfrac{abc}{ab+abc}+\dfrac{1}{a+1}\right)=\dfrac{1}{4}\left(\dfrac{c}{c+1}+\dfrac{1}{a+1}\right)\)
Chứng minh tương tự: \(\dfrac{1}{bc+b+2}\le\dfrac{1}{4}\left(\dfrac{a}{a+1}+\dfrac{1}{b+1}\right);\dfrac{1}{ca+c+2}\le\dfrac{1}{4}\left(\dfrac{b}{b+1}+\dfrac{1}{c+1}\right)\)
Cộng vế theo vế, ta được
\(\dfrac{1}{ab+a+2}+\dfrac{1}{bc+b+2}+\dfrac{1}{ca+c+2}\\ \le\dfrac{1}{4}\left(\dfrac{a+1}{a+1}+\dfrac{b+1}{b+1}+\dfrac{c+1}{c+1}\right)=\dfrac{1}{4}\cdot3=\dfrac{3}{4}\)
Dấu \("="\Leftrightarrow a=b=c=1\)