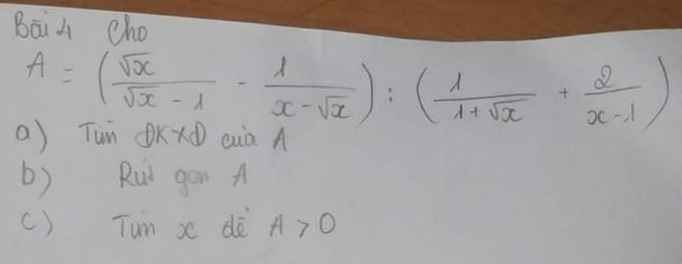a)ĐK:\(\left\{{}\begin{matrix}x-\sqrt{x}\ne0\\x\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\left(\sqrt{x}-1\right)\ne0\\x\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x}\ne0\\\sqrt{x}-1\ne0\\x\ge0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne1\\x\ge0\end{matrix}\right.\)
\(\Rightarrow x\ge0;x\ne1\)
Vậy...
b)\(A=\left(\dfrac{x}{\sqrt{x}\left(\sqrt{x}-1\right)}-\dfrac{1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\)
\(\Leftrightarrow A=\dfrac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}:\dfrac{\sqrt{x}-1+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}\left(\sqrt{x}-1\right)}.\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}+1}\)
\(\Leftrightarrow A=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\sqrt{x}}=\dfrac{x-1}{\sqrt{x}}\)
c)\(A>0\Leftrightarrow\dfrac{x-1}{\sqrt{x}}>0\)\(\Leftrightarrow x-1>0\)(vì\(\sqrt{x}>0\forall x\) thỏa mãn đk)
\(\Leftrightarrow\) x>1
Vậy x>1 thì A>0