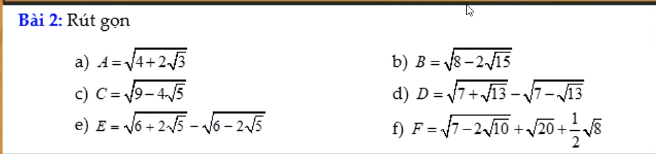Question

Answer 1

 

Answer 2

a) A= \(\sqrt{4+2\sqrt{3}}\)

      = \(\sqrt{3+1+2\sqrt{3}.\sqrt{1}}\)

      = \(\sqrt{\left(\sqrt{3}+\sqrt{1}\right)^2}\)

      = \(\left|\sqrt{3}+1\right|\)

      = \(\sqrt{3}+1\)

 

 

 

Answer 3

a) \(A=\sqrt{4+2\sqrt{3}}=\sqrt{3}+1\)

b) \(B=\sqrt{8-2\sqrt{15}}=\sqrt{5}-\sqrt{3}\)

c) \(C=\sqrt{9-4\sqrt{5}}=\sqrt{5}-2\)

d) \(D=\sqrt{7+\sqrt{13}}-\sqrt{7-\sqrt{13}}\)

\(=\dfrac{\sqrt{14+2\sqrt{13}}-\sqrt{14-2\sqrt{13}}}{\sqrt{2}}\)

\(=\dfrac{\sqrt{13}+1-\sqrt{13}+1}{\sqrt{2}}\)

\(=\sqrt{2}\)