(a) \(a=\dfrac{v-v_0}{t}=\dfrac{12-10}{5}=0,4\left(m/s^2\right)\).

(b) \(t=\dfrac{v'-v}{a'}=\dfrac{0-12}{-0,4}=30\left(s\right)\)

Bài 9. Phương trình có hai nghiệm phân biệt khi:

\(\Delta'=b'^2-ac>0\Leftrightarrow\left(-m\right)^2-1\left(2m-10\right)>0\)

\(\Leftrightarrow m^2-2m+10>0\Leftrightarrow\left(m-1\right)^2+9>0\left(LĐ\right)\)

Phương trình có hai nghiệm phân biệt với mọi \(m.\)

Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m\left(1\right)\\x_1x_2=\dfrac{c}{a}=2m-10\left(2\right)\end{matrix}\right.\)

Theo đề: \(2x_1+x_2=-4\Leftrightarrow x_1+\left(x_1+x_2\right)=-4\)

\(\Leftrightarrow x_1=-4-2m\left(3\right)\)

Thay (3) vào (1) và (2): \(\left\{{}\begin{matrix}-4-2m+x_2=2m\\\left(-4-2m\right)x_2=2m-10\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x_2=4m+4\\x_2=\dfrac{2m-10}{-4-2m}\end{matrix}\right.\)

Suy ra: \(4m+4=\dfrac{10-2m}{2m+4}\Leftrightarrow4m+4=\dfrac{5-m}{m+2}\)

\(\Leftrightarrow4m^2+13m+3=0\) \(\Rightarrow\left[{}\begin{matrix}m=-\dfrac{1}{4}\\m=-3\end{matrix}\right.\).

Vậy: \(m\in\left\{-3;-\dfrac{1}{4}\right\}\)

Bài 10. Phương trình có hai nghiệm khi:

\(\Delta'=b'^2-ac>0\Leftrightarrow\left[-\left(m-1\right)\right]^2-m>0\)

\(\Leftrightarrow m^2-3m+1>0\Leftrightarrow\left[{}\begin{matrix}m< \dfrac{3-\sqrt{5}}{2}\\m>\dfrac{3+\sqrt{5}}{2}\end{matrix}\right.\)

Theo định lí Vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\left(m-1\right)\\x_1x_2=\dfrac{c}{a}=m\end{matrix}\right.\)

Theo đề, \(x_1=1\Rightarrow\left\{{}\begin{matrix}1+x_2=2\left(m-1\right)\\x_2=m\end{matrix}\right.\Rightarrow x_2=3\)

Vậy: Nghiệm còn lại của phương trình là \(x_2=3.\)

Bạn tự vẽ mạch điện theo bài hướng dẫn dưới đây nhé.

Loại trường hợp mắc song song hai đèn vì \(U_{đm_1}\ne U_{đm_2}\ne U=15\left(V\right)\).

Xét trường hợp mắc nối tiếp:

\(\left\{{}\begin{matrix}I_{đm_1}=\dfrac{P_{đm_1}}{U_{đm_1}}=\dfrac{3}{6}=0,5\left(A\right)\\I_{đm_2}=\dfrac{P_{đm_2}}{U_{đm_2}}=\dfrac{6}{9}=\dfrac{2}{3}\left(A\right)\end{matrix}\right.\Rightarrow I_{đm_1}< I_{đm_2}\)

Mà \(U_{đm_1}+U_{đm_2}=6+9=15=U\)

Do đó, mạch có cấu trúc \(\left(Đ_1\left|\right|R_b\right)nt\text{ }Đ_2\) với \(R_b\) là biến trở.

(b) \(R_1=\dfrac{U_{đm_1}^2}{P_{đm_1}}=\dfrac{6^2}{3}=12\left(\Omega\right)\)

\(R_2=\dfrac{U_{đm_2}^2}{P_{đm_2}}=\dfrac{9^2}{6}=13,5\left(\Omega\right)\)

Cường độ dòng điện qua biến trở: \(I_b=I_2-I_1=\dfrac{2}{3}-0,5=\dfrac{1}{6}\left(A\right)\)

Do đèn sáng bình thường: \(U_1=U_{đm_1}=U_b=6\left(V\right)\)

\(R_b=\dfrac{U_b}{I_b}=\dfrac{6}{\dfrac{1}{6}}=36\left(\Omega\right)\)

Vậy: \(R_1=12\left(\Omega\right);R_2=13,5\left(\Omega\right);R_b=36\left(\Omega\right)\).

(c) \(H=\dfrac{P_{đm_1}+P_{đm_2}}{UI_2}\cdot100\%=\dfrac{3+6}{15\cdot\dfrac{2}{3}}\cdot100\%=90\left(\%\right)\)

(d) \(S=\dfrac{d^2}{4}\pi=\dfrac{\left(\dfrac{0,6}{1000}\right)^2}{4}\pi=9\cdot10^{-8}\pi\left(m^2\right)\)

\(R_{b\left(Max\right)}=\rho\cdot\dfrac{l}{S}=0,4\cdot10^{-6}\cdot\dfrac{32}{9\cdot10^{-8}\pi}\approx45,27\left(\Omega\right)\)

\(\dfrac{R_b}{R_{b\left(Max\right)}}=\dfrac{36}{45,27}\approx0,8\Rightarrow R_b\approx80\%R_{b\left(Max\right)}\)

(e) \(I=\dfrac{U}{R_1+R_2}=\dfrac{15}{12+13,5}\approx0,59\left(A\right)\)

Do \(I_{đm_1}< I\) nên đèn 1 sáng mạnh, \(I_{đm_2}>I\) nên đèn 2 sáng yếu.

\(\left\{{}\begin{matrix}\hat{A_4}=5\hat{A_3}\\\hat{A_3}+\hat{A_4}=180^o\left(\text{kề bù}\right)\end{matrix}\right.\Rightarrow\hat{A_4}=150^o\).

Từ hình vẽ, suy ra: \(\hat{B_4}=\hat{A_4}=150^o\) (đồng vị).

Gia tốc rơi tự do trên Mặt Trăng: \(g_T=\dfrac{g}{6}\).

Trọng lượng bạn Dũng lúc này: \(P=mg_T=\dfrac{mg}{6}=\dfrac{60\cdot9,8}{6}=98\left(N\right)\)

Chọn B.

B

\(f'\left(x\right)=3x^2-6x\Rightarrow f''\left(x\right)=6x-6\)

Theo đề: \(f''\left(x\right)=0\Leftrightarrow6x-6=0\Leftrightarrow x=1\).

Thay \(x=1\) vào \(f\left(x\right)\) \(\Rightarrow f\left(x\right)=-1\).

Vậy: Tọa độ điểm là \(I\left(1;-1\right)\)

\(h=\dfrac{1}{2}gt^2=\dfrac{1}{2}\cdot10\cdot8^2=320\left(m\right)\)

\(v=gt=10\cdot8=80\left(ms^{-1}\right)\)

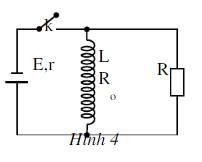
Cho mạch điện như hình vẽ: Ống dây có hệ số tự cảm \(L=2\mu H\) và điện trở \(R_0=1\Omega\); nguồn điện có suất điện động \(E=3V\) và điện trở trong \(r=0,25\Omega\); điện trở \(R=3\Omega\). Bỏ qua điện trở của các dây nối và khóa \(K\).

1. Khóa \(K\) đóng: Tính cường độ dòng điện qua ống dây, \(R\) và công suất của nguồn.

2. Tính nhiệt lượng tỏa ra trên \(R\) sau khi ngắt khóa \(K\).

(Giúp em ý 2 thôi ạ, em cảm ơn)

Câu 8. \(R_1\left|\right|R_2\)

(a) Cường độ dòng điện qua các điện trở:

\(\left\{{}\begin{matrix}I_1=\dfrac{U}{R_1}=\dfrac{18}{18}=1\left(A\right)\\I_2=\dfrac{U}{R_2}=\dfrac{18}{12}=1,5\left(A\right)\end{matrix}\right.\)

Công suất của mạch: \(P=\dfrac{U^2}{R}=\dfrac{U^2}{\dfrac{R_1R_2}{R_1+R_2}}=\dfrac{18^2}{\dfrac{18\cdot12}{18+12}}=45\left(W\right)\)

(b) \(S=0,01\left(mm^2\right)=10^{-8}\left(m^2\right)\)

Chiều dài dây: \(R_1=\rho\cdot\dfrac{l}{S}\Rightarrow l=\dfrac{R_1S}{\rho}=\dfrac{18\cdot10^{-8}}{1,7\cdot10^{-8}}\approx10,59\left(m\right)\)

(c) Đề sai.