Học tại trường
Chưa có thông tin
Đến từ
Chưa có thông tin , Chưa có thông tin
Số lượng câu hỏi
6
Số lượng câu trả lời
11791
Điểm GP
4420
Điểm SP
8728
Người theo dõi (104)
Đang theo dõi (0)

Câu trả lời:
x = -12 : 2/3
= -18

Câu trả lời:
a) Bảng giá trị:
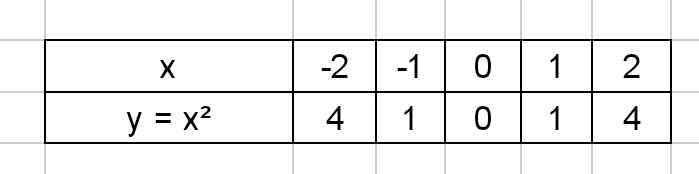 Đồ thị:
Đồ thị:
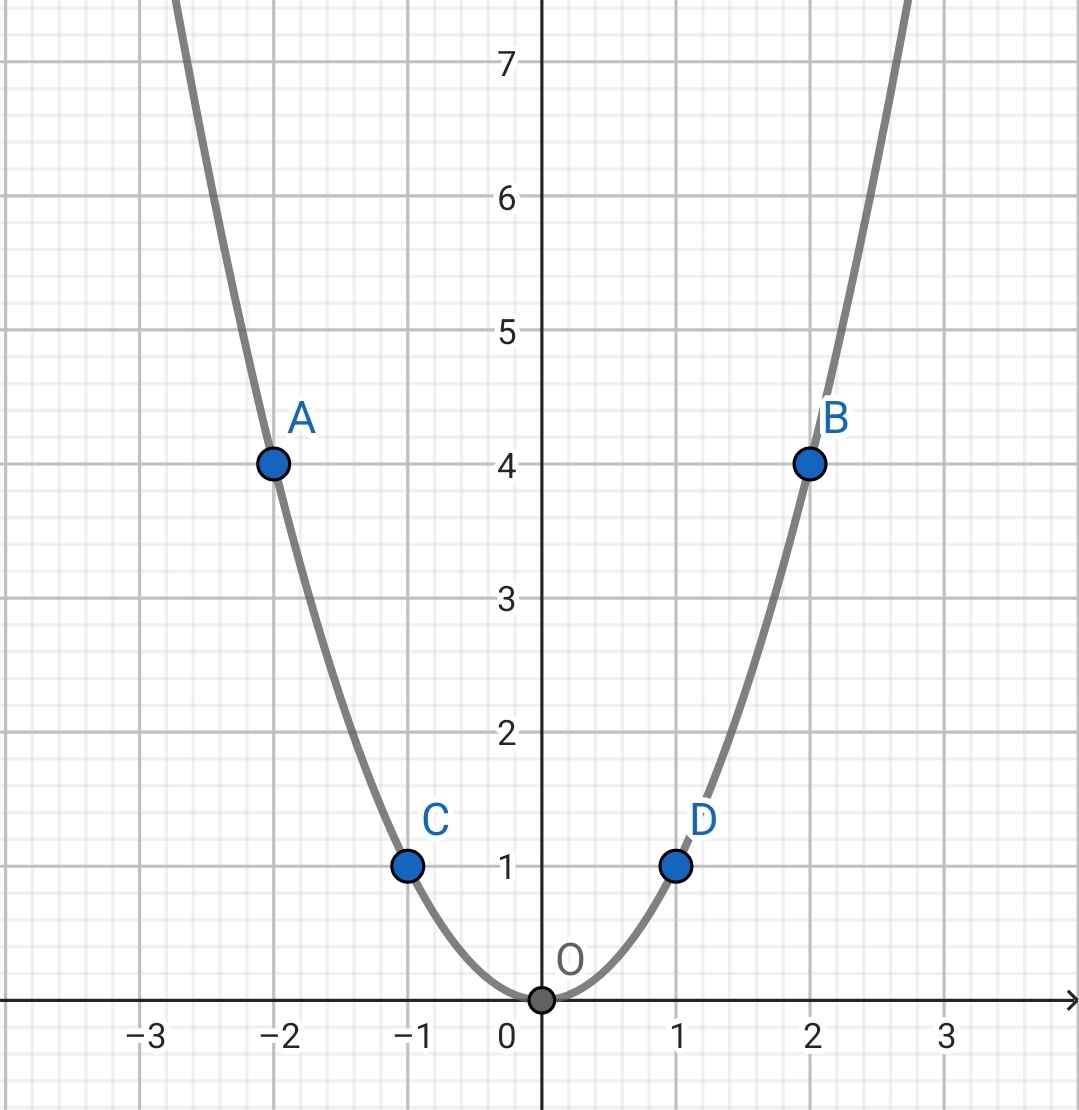

Câu trả lời:
f(2) = 1/2 . 2² = 2
f(-4) = 1/2 . (-4)² = 8

Câu trả lời:
Em ghi đề rõ ràng lại đi