Cho hình vẽ:
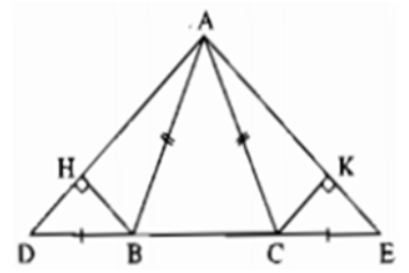
Chọn khẳng định đúng
\(\Delta HAB=\Delta AKC\).\(\Delta ABH=\Delta AKC\).\(\Delta AHB=\Delta ACK\).\(\Delta AHB=\Delta AKC\).Hướng dẫn giải:Có: \(AB=AC\) \(\Rightarrow\) \(\Delta ABC\) cân tại \(A\) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}\) (1)
Lại có: \(\widehat{ABC}+\widehat{ABD}=180^0\) (hai góc kề bù) \(\Rightarrow\) \(\widehat{ABD}=180^0-\widehat{ABC}\) (2)
\(\widehat{ACB}+\widehat{ACE}=180^0\) (hai góc kề bù) \(\Rightarrow\) \(\widehat{ACE}=180^0-\widehat{ACB}\) (3)
Từ (1), (2), (3) \(\Rightarrow\) \(\widehat{ABD}=\widehat{ACE}\)
Khi đó ta chứng minh được \(\Delta ABD=\Delta ACE\) (c.g.c) \(\Rightarrow\) \(\widehat{DAB}=\widehat{EAC}\) (hai góc tương ứng)
Xét \(\Delta AHB\) và \(\Delta AKC\) có:
\(\widehat{H}=\widehat{K}=90^0\)
\(AB=AC\)
\(\widehat{HAB}=\widehat{KAC}\) (do \(\widehat{DAB}=\widehat{EAC}\))
\(\Rightarrow\) \(\Delta AHB=\Delta AKC\) (cạnh huyền - góc nhọn)

