Cho hình lập phương \(ABCD.A'B'C'D'\). Xét \(mp\left(A'BD\right)\). Trong các mệnh đề sau mệnh đề nào đúng?
Góc giữa \(mp\left(A'BD\right)\) và các mặt phẳng chứa các cạnh của hình lập phương bằng \(\alpha\) mà \(tan\alpha=\dfrac{1}{\sqrt{2}}\).Góc giữa \(mp\left(A'BD\right)\) và các mặt phẳng chứa các cạnh của hình lập phương bằng \(\alpha\) mà \(sin\alpha=\dfrac{1}{\sqrt{3}}\).Góc giữa \(mp\left(A'BD\right)\) và các mặt phẳng chứa các cạnh của hình lập phương bằng \(\alpha\) với \(\alpha\) phụ thuộc vào kích thước của hình lập phương.Góc giữa \(mp\left(A'BD\right)\) và các mặt phẳng chứa các cạnh của hình lập phương bằng \(\alpha\) với \(cos\alpha=\dfrac{\sqrt{3}}{3}\).Hướng dẫn giải: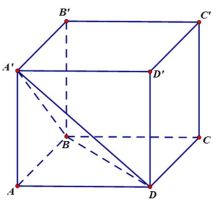
ABCD.A'B'C'D' là hình lập phương nên hình chiếu của tam giác A'BD lên các mặt chứa các cạnh của hình lập phương là tam giác bằng nhau. Gọi diện tích tam giác này là \(S_1\) thì \(S_1=S_{AB'D.}cos\alpha\).
Do đó góc giữa \(mp\left(A'BD\right)\) và các mặt phẳng chứa các cạnh của hình lập phương bằng nhau.
\(A'B'=BD=A'D=\sqrt{2}a\) .
Suy ra tam giác A'BD đều và có diện tích là: \(\dfrac{1}{2}A'B.A'D.sin60^o=\dfrac{1}{2}.\sqrt{2}a.\sqrt{2}a=\dfrac{\sqrt{3}}{2}a^2\).
Hình chiếu của tam giác A'BD lên mặt phẳng (A'ADD') là tam giác A'AD.
\(S_{\Delta AA'D}=\dfrac{1}{2}a^2\).
Suy ra \(cos\alpha=\dfrac{S_{\Delta AA'D}}{S_{\Delta A'B'D}}=\dfrac{\dfrac{1}{2}a^2}{\dfrac{\sqrt{3}}{2}a^2}=\dfrac{\sqrt{3}}{3}\).

