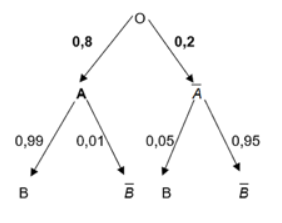
Với giả thiết như phần vận dụng:
a) Hãy ước lượng tỉ lệ cây con có kiểu gene BB.
b) Sử dụng kết quả của vận dụng trên và câu a, hãy ước lượng tỉ lệ cây con có kiểu gene Bb.
Giả thiết: Hình dạng hạt của đậu Hà Lan có hai kiểu hình: hạt trơn và hạt nhẵn, có hai gene ứng với hai kiểu hình này là gene trội B và gene lặn b.
Khi cho lai hai cây đậu Hà Lan, cây con lấy ngẫu nhiên một cách độc lập một gene từ cây bố và một gene từ cây mẹ để hình thành một cặp gene. Giả sử cây bố và cây mẹ được chọn ngẫu nhiên từ một quần thể các cây đậu Hà Lan, ở đó tỉ lệ cây mang kiểu gene bb, Bb tương ứng là 40% và 60%.