Tính vận tốc tức thời của viên bi tại thời điểm \({x_0} = 1s\) trong bài toán tìm vận tốc tức thời
Bài 1. Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm
Giải mục 1 trang 60 ,Hoạt động 1 (SGK Cánh Diều)
Thảo luận (1)
Giải mục 1 trang 60 ,Luyện tập – Vận dụng 1 (SGK Cánh Diều)
Tính đạo hàm của hàm số \(f\left( x \right) = 2x\)tại \({x_0} = 3\) bằng định nghĩa
Thảo luận (1)Hướng dẫn giải\(f'\left(3\right)=\lim\limits_{x\rightarrow3}\dfrac{f\left(x\right)-f\left(3\right)}{x-3}\\ =\lim\limits_{x\rightarrow3}\dfrac{2x-6}{x-3}\\ =2\)
(Trả lời bởi Hà Quang Minh)
Giải mục 1 trang 60 ,Luyện tập và vận dụng 2 (SGK Cánh Diều)
Tính đạo hàm của hàm số \(f\left( x \right) = {x^3}\) tại điểm x bất kì bằng định nghĩa
Thảo luận (1)Hướng dẫn giảiXét \(\Delta x\) là số gia của biến số tại điểm x
Ta có:
\(\begin{array}{l}\Delta y = f\left( {x + \Delta x} \right) - f\left( x \right) = {\left( {x + \Delta x} \right)^3} - {x^3} = \left( {x + \Delta x - x} \right)\left[ {x{{\left( {x + \Delta x} \right)}^2} + x.\left( {x + \Delta x} \right) + {x^2}} \right]\\ = \Delta x\left( {{x^2} + 2x.\Delta x + {{\left( {\Delta x} \right)}^2} + {x^2} + x.\Delta x + {x^2}} \right) = \Delta x.\left( {3{x^2} + {{\left( {\Delta x} \right)}^2} + 3x.\Delta x} \right)\\ \Rightarrow \frac{{\Delta y}}{{\Delta x}} = 3{x^2} + {\left( {\Delta x} \right)^2} + 3x.\Delta x\end{array}\)
Ta thấy:
\(\begin{array}{l}\mathop {\lim }\limits_{\Delta x \to 0} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{\Delta x \to 0} \left( {3{x^2} + {{\left( {\Delta x} \right)}^2} + 3x.\Delta x} \right) = 3{x^2}\\ \Rightarrow f'\left( x \right) = 3{x^2}\end{array}\)
(Trả lời bởi Quoc Tran Anh Le)
Hoạt động 2,Giải mục 2 trang 62 (SGK Cánh Diều)
Cho hàm số y f(x) có đồ thị (C), một điểm {M_0} cố định thuộc (C) có hoành độ {x_0}. Với mỗi điểm M thuộc (C) khác {M_0}, kí hiệu {x_M} là hoành độ của điểm M và {k_M} là hệ số góc của cát tuyến {M_0}M. Giả sử tồn tại giới hạn hữu hạn {k_0} mathop {lim }limits_{{x_M} to {x_0}} {k_M}. Khi đó, ta coi đường thẳng {M_0}T đi qua {M_0} và có hệ số góc là {k_0} là ví trị giới hạn của cát tuyến {M_0}M khi điểm M di chuyển dọc theo (C) dần tới {M_0} . Đường thẳng {M_0}Tđược gọi là tiếp tuyến của (C) tạ...
Đọc tiếp
Cho hàm số y = f(x) có đồ thị (C), một điểm \({M_0}\) cố định thuộc (C) có hoành độ \({x_0}\). Với mỗi điểm M thuộc (C) khác \({M_0}\), kí hiệu \({x_M}\) là hoành độ của điểm M và \({k_M}\) là hệ số góc của cát tuyến \({M_0}M\). Giả sử tồn tại giới hạn hữu hạn \({k_0} = \mathop {\lim }\limits_{{x_M} \to {x_0}} {k_M}\). Khi đó, ta coi đường thẳng \({M_0}T\) đi qua \({M_0}\) và có hệ số góc là \({k_0}\) là ví trị giới hạn của cát tuyến \({M_0}M\) khi điểm M di chuyển dọc theo (C) dần tới \({M_0}\) . Đường thẳng \({M_0}T\)được gọi là tiếp tuyến của (C) tại điểm \({M_0}\), còn \({M_0}\) được gọi là tiếp điểm (Hình 3).
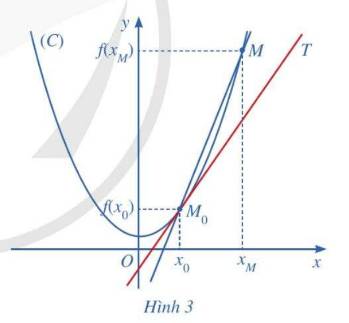
a) Xác định hệ số góc \({k_0}\) của tiếp tuyến \({M_0}T\) theo \({x_0}\)
b) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\)
Thảo luận (1)Hướng dẫn giảia) \({k_0} = \mathop {\lim }\limits_{x \to {x_M}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = f'({x_0})\)
b) Phương tình tiếp tuyến của đồ thị hàm số tại điểm \({M_0}\):
\(y = {k_0}(x - {x_0}) + {y_0}\)
(Trả lời bởi Quoc Tran Anh Le)
Luyện tập – Vận dụng 3,Giải mục 2 trang 62 (SGK Cánh Diều)
Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{1}{x}\) tại điểm N (1; 1)
Thảo luận (1)Hướng dẫn giải\(y'\left(1\right)=-\dfrac{1}{1^2}=-1\)
Phương trình tiếp tuyến của đồ thị hàm số tại điểm N(1;1) là:
\(y=-1\left(x-1\right)+1=-x+2\)
(Trả lời bởi Hà Quang Minh)
Bài 1 trang 63 (SGK Cánh Diều)
Đề bài
Tính đạo hàm của hàm số \(f(x) = 3{x^3} - 1\) tại điểm \({x_0} = 1\) bằng định nghĩa
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}\Delta x = x - {x_0} = x - 1\\\Delta y = f({x_0} + \Delta x) - f({x_0}) = f(x) - f(1)\\\mathop {\lim }\limits_{x \to 1} \frac{{\Delta y}}{{\Delta x}} = \mathop {\lim }\limits_{x \to 1} \frac{{f(x) - f(1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{3{x^3} - 1 - (3 - 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} \frac{{3{x^3} - 3}}{{x - 1}}\\ = \mathop {\lim }\limits_{x \to 1} \frac{{3(x - 1)({x^2} + x + 1)}}{{x - 1}} = \mathop {\lim }\limits_{x \to 1} (3({x^2} + x + 1)) = 9\end{array}\)
Vậy \(f'(1) = 9\)
(Trả lời bởi Quoc Tran Anh Le)
Bài 2 trang 63 (SGK Cánh Diều)
Đề bài
Chứng minh rằng hàm số \(f(x) = \left| x \right|\) không có đạo hàm tại điểm \({x_0} = 0\), nhưng có đạo hàm tại mọi điểm \(x \ne 0\)
Thảo luận (1)Hướng dẫn giải\(y = \left| x \right| = \left\{ \begin{array}{l}x\,\,\,(x \ge 0)\\ - x\,\,\,(x < 0)\end{array} \right. \Rightarrow y' = \left\{ \begin{array}{l}1\,\,\,(x \ge 0)\\ - 1\,\,\,(x < 0)\end{array} \right.\)
Ta có: \(\mathop {\lim }\limits_{x \to {0^ + }} y' = 1 \ne - 1 = \mathop {\lim }\limits_{x \to {0^ - }} y'\)
Vậy không tồn tại đạo hàm của hàm số tại x = 0
(Trả lời bởi Quoc Tran Anh Le)
Bài 3 trang 63 (SGK Cánh Diều)
Đề bài
Cho hàm số \(y = - 2{x^2} + x\) có đồ thị (C).
a) Xác định hệ số góc của tiếp tuyến của đồ thị (C) tại điểm có hoành độ bằng 2
b) Viết phương trình tiếp tuyến của đồ thị (C) tại điểm M(2; - 6)
Thảo luận (1)Hướng dẫn giảia, Hệ số góc của tiếp tuyến của đồ thị là:
\(y'\left(2\right)=-4\cdot2+1=-7\)
b, Phương trình tiếp tuyến của đồ thị (C) tại điểm M(2;-6) là:
\(y=y'\left(2\right)\cdot\left(x-2\right)-6=-7\left(x-2\right)-6=-7x+8\)
(Trả lời bởi Hà Quang Minh)
Bài 4 trang 63 (SGK Cánh Diều)
Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là C(Q) {Q^2} + 80Q + 3500a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm đượcc) Hãy tính chi phí sản xuất máy vô tuyến thứ 100
Đọc tiếp
Giả sử chi phí C (USD) để sản xuất Q máy vô tuyến là \(C(Q) = {Q^2} + 80Q + 3500\)
a) Ta gọi chi phí biên là chi phí gia tăng để sản xuất thêm 1 sản phẩm từ Q sản phẩm lên Q + 1 sản phẩm. Giả sử chi phí biên được xác định bởi hàm số C’(Q). Tìm hàm chi phí biên.
b) Tìm C’(90) và giải thích ý nghĩa kết quả tìm được
c) Hãy tính chi phí sản xuất máy vô tuyến thứ 100
Thảo luận (1)Hướng dẫn giảia, Hàm chi phí biên là:
\(C'\left(Q\right)=2Q+80\)
b, \(C'\left(90\right)=2\cdot90+80=260\left(USD\right)\)
Ý nghĩa: Chi phí gia tăng để sản xuất thêm 1 sản phẩm từ 89 sản phẩm lên 90 sản phẩm là 260 (USD)
c, Chi phí sản xuất máy vô tuyến thứ 100 là:
\(C'\left(100\right)=2\cdot100+80=280\left(USD\right)\)
(Trả lời bởi Hà Quang Minh)