Xem các hình 156, 157, 158 và trả lời các câu hỏi sau :
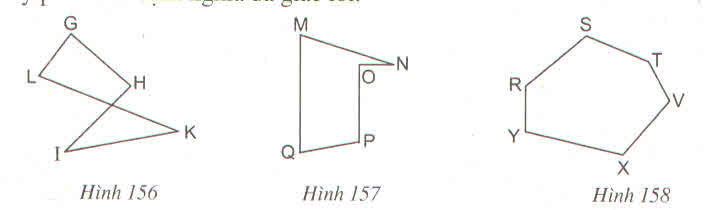
a) Vì sao hình năm cạnh GHIKL (h.156) không phải là đa giác lồi ?
b) Vì sao hình năm cạnh MNOPQ (h.157) không phài là đa giác lồi ?
c) Vì sao hình sáu cạnh RSTVXY (h.158) là một đa giác lồi ?
Hãy phát biểu định nghĩa đa giác lồi ?