Cho tam giác ABC có \(\widehat {BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.
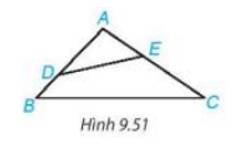
Cho tam giác ABC có \(\widehat {BAC}\) là góc tù. Lấy điểm D nằm giữa A và B, lấy điểm E nằm giữa A và C (H.9.51). Chứng minh DE < BC.

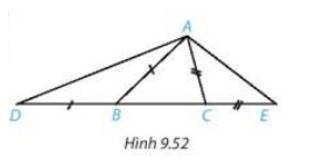
Cho tam giác ABC ( AB > AC). Trên đường thẳng chứa cạnh BC, lấy điểm D và điểm E sao cho B nằm giữa D và C, C nằm giữa B và E, BD = BA, CE = CA ( H.9.52)
a) So sánh \(\widehat {ADE}\) và \(\widehat {AED}\).
b) So sánh các đoạn thẳng AD và AE.
Thảo luận (1)Hướng dẫn giảia)
\(AB > AC \Rightarrow \widehat {ABC} < \widehat {ACB}\)( quan hệ giữa góc và cạnh đối diện trong tam giác ABC)
\(\begin{array}{l} \Rightarrow {180^0} - \widehat {ABD} < {180^0} - \widehat {ACE}\\ \Rightarrow \widehat {ABD} > \widehat {ACE}\end{array}\)
Vì BD= BA nên tam giác ABD cân tại B \( \Rightarrow \widehat {ABD} = {180^0} - 2\widehat {ADB}\)
Vì CE = CA nên tam giác ACE cân tại C \( \Rightarrow \widehat {ACE} = {180^0} - 2\widehat {AEC}\)
\(\begin{array}{*{20}{l}}{ \Rightarrow {{180}^0} - 2\widehat {ADB} > {{180}^0} - 2\widehat {AEC}}\\{ \Rightarrow \widehat {ADB} < \widehat {AEC}}\\{Hay{\mkern 1mu} \widehat {ADE} < \widehat {AED}}\end{array}\)
b) Xét tam giác ADE ta có : \(\widehat {ADB} < \widehat {AEC}\)
\( \Rightarrow AD > AE\)(Quan hệ giữa cạnh và góc đối diện trong tam giác).
(Trả lời bởi Hà Quang Minh)
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a)\(AI < \dfrac{1}{2}\left( {AB + AC} \right)\)
b)\(AM < \dfrac{1}{2}\left( {AB + AC} \right)\)
Thảo luận (1)Hướng dẫn giải
a)
AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)
b)
Lấy D sao cho M là trung điểm của AD
Xét \(\Delta ABM\) và \(DCM\) có
AM = DM ( do M là trung điểm của AD)
BM = CM ( do M là trung điểm của BC)
\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)
\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)
\( \Rightarrow AB = CD\)(2 cạnh tương ứng)
Xét \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)
\( \Rightarrow \) 2AM < AC + AB
\( \Rightarrow \) AM < \(\dfrac{1}{2}\)(AB + AC)
(Trả lời bởi Kiều Sơn Tùng)
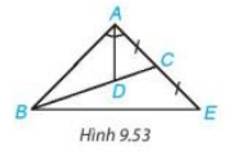
Cho tam giác ABC có đường phân giác AD, D nằm trên BC sao cho BD= 2 DC. Trên đường thẳng AC, lấy điểm E sao cho C là trung điểm của AE (H.9.53). Chứng minh rằng tam giác ABE cân tại A
Gợi ý D là trọng tâm của tam gíac ABE, tam giác này có đường phân giác AD đồng thời là trung tuyến.
Thảo luận (1)Hướng dẫn giảiC là trung điểm của AE
\( \Rightarrow \) BC là trung tuyến của tam giác ABE (1)
D thuộc BC, \(BD = 2DC \Rightarrow BD = 2\left( {BC - BD} \right) \Rightarrow 3BD = 2BC \Rightarrow BD = \dfrac{2}{3}BC\)(2)
Từ (1) và (2) suy ra: D là trọng tâm của tam giác ABE
\( \Rightarrow \) AD là đường trung tuyến ứng với BE
Mà AD là đường phân giác của \(\widehat {BAC}\)
\( \Rightarrow \) Tam giác ABE cân tại A.
(Trả lời bởi Hà Quang Minh)
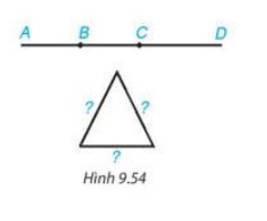
Một sợ dây thép dài 1,2m. Cần đánh dấu trên sợ dây thép đó hai điểm để khi uốn gập nó lại tại hai điểm đó sẽ tạo thành tam giác cân có một cạnh bằng 30 cm (h.9.54). Em hãy mô tả các cách đánh dấu hai điểm trên sợi dây thép.
Thảo luận (1)Hướng dẫn giảiTH1: Cạnh bên bằng 30 cm
Khi đó cạnh đáy bằng: 120 – (30 + 30 ) =60 (cm)
Vì 30 + 30 = 60 nên bộ 3 độ dài này không tạo được thành tam giác.
TH2: Cạnh đáy bằng 30 cm
Khi đó cạnh bên bằng: (120 – 30) : 2 = 45 (cm)
Đánh dấu AB = CD = 45 cm.
(Trả lời bởi Hà Quang Minh)