Gieo một con xúc xắc 50 lần cho kết quả như sau:

Tần số xuất hiện của mặt 3 chấm là
A. 9. B. 10. C. 11. D. 12.
Gieo một con xúc xắc 50 lần cho kết quả như sau:

Tần số xuất hiện của mặt 3 chấm là
A. 9. B. 10. C. 11. D. 12.
Gieo một con xúc xắc 50 lần cho kết quả như sau:

Tần số tương đối xuất hiện của mặt 5 chấm là
A. 6%. B. 8%. C. 12%. D. 14%.
Thảo luận (1)Hướng dẫn giảiTần số tương đối xuất hiện của mặt 5 chấm là: \(\frac{6}{{50}} = 12\% \)
Chọn C
(Trả lời bởi datcoder)
Gieo một con xúc xắc 50 lần cho kết quả như sau:

Để biểu diễn bảng thống kê trên, không thể dùng loại biểu đồ nào sau đây?
A. Biểu đồ tranh.
B. Biểu đồ tần số dạng cột.
C. Biểu đồ tần số dạng đoạn thẳng.
D. Biểu đồ cột kép.
Thảo luận (1)Hướng dẫn giảiKhông thể dùng biểu đồ cột kép để biểu diễn bảng thống kê trên vì biểu đồ cột kép dùng để hai dữ liệu cùng loại trở lên, còn bảng thống kê này chỉ có 1 dữ liệu.
Chọn D
(Trả lời bởi datcoder)
Gieo một con xúc xắc 50 lần cho kết quả như sau:

Để vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng, ta dùng giá trị nào đại diện cho nhóm số liệu [10; 20)?
A. 10. B. 15. C. 20. D. 30.
Thảo luận (1)Hướng dẫn giảiGiá trị đại diện cho nhóm số liệu \(\left[ {10;20} \right)\) là: \(\frac{{10 + 20}}{2} = 15\)
Chọn B
(Trả lời bởi datcoder)
Biểu đồ tần số tương đối ghép nhóm Hình 7.22 cho biết tỉ lệ chiều cao của các cây keo giống do một kĩ dư lâm nghiệp đã trồng trong nhà kính.
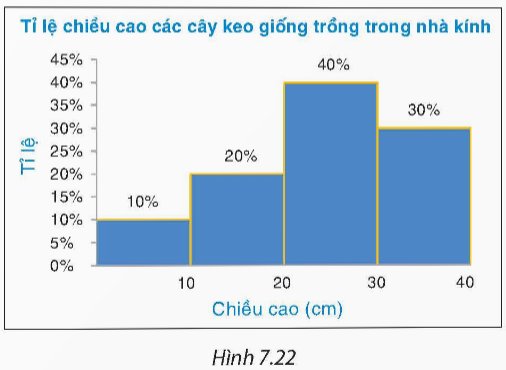
Lập bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ.
Thảo luận (1)Hướng dẫn giảiTừ biểu đồ tần số tương đối ta có, có 10% số cây có chiều cao từ 0cm đến dưới 10cm; 20% số cây có chiều cao từ 10cm đến dưới 20cm; 40% số cây có chiều cao từ 20cm đến dưới 30cm; 30% số cây có chiều cao từ 30cm đến dưới 40cm.
Ta có bảng tần số tương đối ghép nhóm cho dữ liệu được biểu diễn trên biểu đồ là:
(Trả lời bởi datcoder)
Chiều cao (cm) [0;10) [10;20) [20;30) [30;40) Tần số tương đối 10% 20% 40% 30%
Kĩ sư lâm nghiệp trên cũng trồng một số cây keo giống khác ngoài trời thu được kết quả như sau:

a) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê trên.
b) Từ biểu đồ vừa vẽ và biểu đồ cho trong bài tập 7.26, hãy so sánh chiều cao của các cây keo giống được trồng trong nhà kính và trồng ngoài trời.
Thảo luận (1)Hướng dẫn giảia) Tổng số cây là: \(5 + 9 + 4 + 2 = 20\) (cây)
Tần số tương đối của các cây có chiều cao \(\left[ {0;10} \right)\); \(\left[ {10;20} \right)\); \(\left[ {20;30} \right)\); \(\left[ {30;40} \right)\) lần lượt là: \(\frac{5}{{20}} = 25\% ;\frac{9}{{20}} = 45\% ;\frac{4}{{20}} = 20\% ;\frac{2}{{20}} = 10\% \)
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
b) Với chiều cao thuộc nhóm \(\left[ {0;10} \right)\): Số cây ngoài trời nhiều hơn số cây trong nhà kính.
Với chiều cao thuộc nhóm \(\left[ {10;20} \right)\): Số cây ngoài trời nhiều hơn số cây trong nhà kính.
Với chiều cao thuộc nhóm \(\left[ {20;30} \right)\): Số cây ngoài trời ít hơn số cây trong nhà kính.
Với chiều cao thuộc nhóm \(\left[ {30;40} \right)\): Số cây ngoài trời ít hơn số cây trong nhà kính.
(Trả lời bởi datcoder)
Tỉ lệ học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường được cho trong bảng sau:

Biết rằng có 500 học sinh tham gia bình chọn.
a) Vẽ biểu đồ hình quạt tròn biểu diễn bảng tần số tương đối trên.
b) Lập bảng tần số biểu diễn số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường.
Thảo luận (1)Hướng dẫn giảia) Bước 1: Xác định số đo cung tương ứng của các hình quạt biểu diễn các tần số tương đối của tỉ lệ bình chọn cầu thủ xuất sắc nhất:
Huy: \({360^o}.30\% = {108^o}\), Minh: \({360^o}.25\% = {90^o}\), An: \({360^o}.10\% = {36^o}\), Thảo: \({360^o}.35\% = {126^o}\).
Bước 2: Vẽ hình tròn và chia hình tròn thành các hình quạt.
Bước 3: Định dạng các hình quạt tròn, ghi tần số tương đối, chú giải và tiêu đề.
b) Số học sinh bình chọn Huy là cầu thủ xuất sắc nhất là: \(500.30\% = 150\) (học sinh)
Số học sinh bình chọn Minh là cầu thủ xuất sắc nhất là: \(500.25\% = 125\) (học sinh)
Số học sinh bình chọn An là cầu thủ xuất sắc nhất là: \(500.10\% = 50\) (học sinh)
Số học sinh bình chọn Thảo là cầu thủ xuất sắc nhất là: \(500.35\% = 175\) (học sinh)
Ta có bảng tần số biểu diễn số học sinh bình chọn cho danh hiệu cầu thủ xuất sắc nhất trong giải bóng đá của trường là:
(Trả lời bởi datcoder)
Cầu thủ Huy Minh An Thảo Số học sinh bình chọn 150 125 50 175
Qua đợt khám mắt, lớp 9A có 20 học sinh bị cận thị trong đó có 10 học sinh cận thị nhẹ, 8 học sinh cận thị vừa và 2 học sinh cận thị nặng. Biết rằng cận thị có số đo từ 0,25 đến dưới 3,25 dioptre là cận thị nhẹ; từ 3,25 đến dưới 6,25 dioptre là cận thị vừa; từ 6,25 đến dưới 10,25 dioptre là cận thị nặng.
a) Lập bảng tần số và bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng cho bảng tần số tương đối ghép nhóm thu được ở câu a.
Thảo luận (1)Hướng dẫn giảia) Vì có 10 học sinh có số đo từ 0,25 đến dưới 3,25 dioptre; 8 học sinh có số đo từ 3,25 đến dưới 6,25 dioptre và 2 học sinh có số đo từ 6,25 đến dưới 10,25 dioptre nên ta có bảng tần số ghép nhóm:
Độ cận (dioptre) [0,25;3,25) [3,25;6,25) [6,25;10,25) Số học sinh 10 8 2 Tần số tương đối của các nhóm \(\left[ {0,25;3,25} \right)\); \(\left[ {3,25;6,25} \right)\); \(\left[ {6,25;10,25} \right)\) lần lượt là: \(\frac{{10}}{{20}} = 50\% ;\frac{8}{{20}} = 40\% ;\frac{2}{{20}} = 10\% \)
Ta có bảng tần số tương đối ghép nhóm theo độ cận thị của các học sinh này là:
Độ cận (dioptre) [0,25;3,25) [3,25;6,25) [6,25;10,25) Tần số tương đối 50% 40% 10% b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng đoạn thẳng:
Bước 1: Chọn giá trị đại diện cho các nhóm số liệu ta có bảng sau:
Giá trị đại diện 1,75 4,75 8,25 Tần số tương đối 50% 40% 10% Bước 2: Vẽ các trục.
Bước 3: Xác định các điểm, nối các điểm liên tiếp với nhau.
Bước 4: Ghi chú giải cho các trục, các điểm và tiêu đề của biểu đồ tần số tương đối ghép nhóm.
(Trả lời bởi datcoder)
Lương của các công nhân một nhà máy được cho trong bảng sau:

a) Nêu các nhóm số liệu và tần số. Giải thích ý nghĩa cho một nhóm số liệu và tẩn số của nó.
b) Vẽ biểu đồ tần số tương đối ghép nhóm dạng cột cho bảng thống kê trên.
Thảo luận (1)Hướng dẫn giảia) Các nhóm số liệu về tiền lương \(\left[ {5;7} \right)\); \(\left[ {7;9} \right)\); \(\left[ {9;11} \right)\); \(\left[ {11;13} \right)\); \(\left[ {13;15} \right)\) có tần số lần lượt là 20; 50; 70; 40; 20.
Giải thích ý nghĩa của một nhóm số liệu: Nhóm \(\left[ {5;7} \right)\) có tần số là 20 tức là có 20 công nhân có lương từ 5 triệu đến dưới 7 triệu.
b) Tổng số công nhân là: \(20 + 50 + 70 + 40 + 20 = 200\) (công nhân)
Tần số tương đối của công nhân có lương \(\left[ {5;7} \right)\); \(\left[ {7;9} \right)\); \(\left[ {9;11} \right)\); \(\left[ {11;13} \right)\); \(\left[ {13;15} \right)\) lần lượt là: \(\frac{{20}}{{200}} = 10\% ;\frac{{50}}{{200}} = 25\% ;\frac{{70}}{{200}} = 35\% ;\frac{{40}}{{200}} = 20\% ;\frac{{20}}{{200}} = 10\% \)
Bước 1: Vẽ trục đứng, trục ngang. Trên trục đứng xác định đơn vị độ dài phù hợp với các tần số tương đối. Trên trục ngang xác định các nhóm số liệu cần biểu diễn.
Bước 2: Dựng các hình cột (kề nhau) ứng với các nhóm dữ liệu.
Bước 3: Ghi chú giải cho các trục, các cột và tiêu đề cho biểu đồ.
(Trả lời bởi datcoder)