Chủ đề / Chương

Bài học

Chủ đề

Bài tập cuối chương 4

Câu 1 (SGK Cánh Diều - Tập 1 - Trang 92)

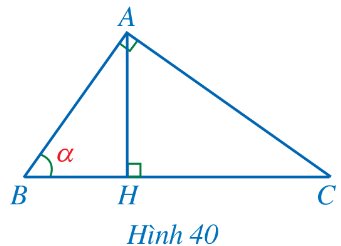
Cho tam giác ABC vuông tại A có đường cao AH và widehat{B}alpha (Hình 40).a) Tỉ số dfrac{HA}{HB} bằngA. sinα.              B. cosα.              C. tanα.              D. cotα.b) Tỉ số dfrac{HA}{HC} bằngA. sinα.              B. cosα.              C. tanα.              D. cotα.c) Tỉ số dfrac{HA}{AC} bằngA. sinα.              B. cosα.              C. tanα.              D. cotα.
Đọc tiếp
Hướng dẫn giải

a) Chọn đáp án C.

b) Xét tam giác \(AHC\) vuông tại \(H\) có:

\(\tan C = \frac{{HA}}{{HC}}\).

Do \(\widehat B + \widehat C = 90^\circ \) nên \(\tan C = \cot B\).

Vậy \(\cot \alpha  = \frac{{HA}}{{HC}}\).

Chọn đáp án D.

c) Xét tam giác \(AHC\) vuông tại \(H\) có:

\(\sin C = \frac{{HA}}{{AC}}\).

Do \(\widehat B + \widehat C = 90^\circ \) nên \(\sin C = \cos B\).

Vậy \(\cos \alpha  = \frac{{HA}}{{AC}}\).

Chọn đáp án B.

(Trả lời bởi datcoder)
Thảo luận (1)

Câu 2 (SGK Cánh Diều - Tập 1 - Trang 92)

Cho hình thoi ABCD có AB = a, \(\widehat{BAD}\) = 2α (0° < α < 90°). Chứng minh:

a) BD = 2a.sinα;

b) AC = 2a.cosα.

Hướng dẫn giải

Do \(\widehat {BAD} = 2\alpha  \Rightarrow \widehat {OAB} = \alpha \).

a) Xét tam giác \(BOA\) vuông tại \(O\) có :

\(BO = AB.\sin \alpha  = a.\sin \alpha \).

Mà \(BD = 2BO = 2a.\sin \alpha \).

b) Xét tam giác \(BOA\) vuông tại \(O\) có:

\(CO = AB.\cos \alpha  = a.\cos \alpha \).

Mà \(AC = 2CO = 2a.\cos \alpha \).

(Trả lời bởi datcoder)
Thảo luận (1)

Câu 3 (SGK Cánh Diều - Tập 1 - Trang 92)

Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) OA = 3 m tạo với phương thẳng đứng một góc là \(\widehat{AOH}\) = 43° thì khoảng cách AH từ em bé đến vị trí cân bằng là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)?

Hướng dẫn giải

Xét tam giác \(OHA\) vuông tại \(H\) ta có:

\(AH = OA.\sin \widehat {AOH} = 3.\sin 43^\circ  \approx 2\left( m \right)\).

Vậy khoảng cách \(AH\) từ em bé đến vị trí cân bằng khoảng 2m.

(Trả lời bởi datcoder)
Thảo luận (1)

Câu 4 (SGK Cánh Diều - Tập 1 - Trang 92)

Một người đứng ở vị trí B trên bờ sông muốn sử dụng la bàn để ước lượng khoảng cách từ vị trí đó đến một vị trí A ở trên một cù lao giữa dòng sông. Người đó đã làm như sau:– Sử dụng la bàn, xác định được phương BA lệch với phương Nam – Bắc về hướng Đông 52°.– Người đó di chuyển đến vị trí C, cách B một khoảng là 187 m. Sử dụng la bàn, xác định được phương CA lệch với phương Nam – Bắc về hướng Tây 27°; CB lệch với phương Nam – Bắc về hướng Tây 70° (Hình 42).Em hãy giúp người đó tính khoảng cách A...
Đọc tiếp
Hướng dẫn giải

Lấy B’B, C’C là các đường thẳng biểu diễn phương Nam – Bắc như hình vẽ.

Theo bài ra ta có \(\widehat {B'BA} = 52^\circ ,\widehat {C'CA} = 27^\circ ,\widehat {C'CB} = 70^\circ \) suy ra \(\widehat {ACB} = \widehat {C'CB} - \widehat {C'CA} = 70^\circ  - 27^\circ  = 43^\circ \).

Kẻ AA’ ( \(A' \in BC\)) song song với phương Nam – Bắc, khi đó \(AA'//BB'//CC'\).

Vì \(AA'//BB'//CC'\) nên ta có \(\widehat {B'BA} = \widehat {BAA'} = 52^\circ \) (hai góc so le trong) và \(\widehat {A'AC} = \widehat {C'CA} = 27^\circ \) suy ra \(\widehat {BAC} = \widehat {BAA'} + \widehat {A'AC} = 52^\circ  + 27^\circ  = 79^\circ \).

Kẻ \(BH \bot AC\left( {H \in AC} \right)\).

Xét \(\Delta BHC\) vuông tại H có: \(\sin C = \frac{{BH}}{{BC}}\) suy ra \(BH = \sin C.BC = \sin 43^\circ .187 \approx 128\left( m \right)\).

Xét \(\Delta BAH\) vuông tại H có: \(\sin A = \frac{{BH}}{{BA}}\) suy ra \(BA = \frac{{BH}}{{\sin A}} \approx \frac{{128}}{{\sin 79^\circ }} \approx 130\left( m \right)\)

Vậy khoảng cách AB là khoảng 130m.

(Trả lời bởi datcoder)
Thảo luận (1)
Bài trước
Bài tiếp theo