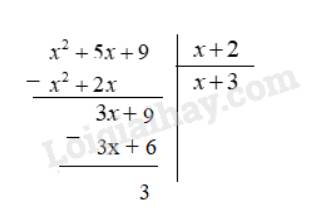Hãy dùng tính chất phân phối để thực hiện phép nhân x.(2x+3)
Bài 4. Phép nhân và phép chia đa thức một biến
Hoạt động 1 (SGK Chân trời sáng tạo trang 37)
Thảo luận (1)
Thực hành 1 (SGK Chân trời sáng tạo trang 37)
Thực hiện phép nhân \((4x - 3)(2{x^2} + 5x - 6)\)
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}(4x - 3)(2{x^2} + 5x - 6)\\ = 4x.2{x^2} + 4x.5x - 6.4x - 3.2{x^2} - 3.5x + 18\\ = 8{x^3} + 20{x^2} - 6{x^2} - 24x - 15x + 18\\ = 8{x^3} + 14{x^2} - 39x + 18\end{array}\)
(Trả lời bởi Hà Quang Minh)
Vận dụng 1 (SGK Chân trời sáng tạo trang 37)
Tìm đa thức theo biến x biểu thị thể tích của hình hộp chữ nhật có kích thước như Hình 2.
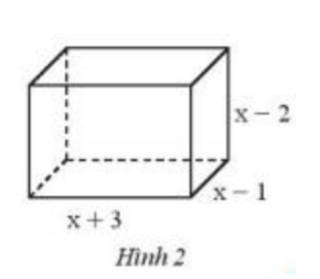
Thảo luận (1)Hướng dẫn giảiThể tích hình hộp chữ nhật là :
\(\begin{array}{l}(x + 3).(x - 1).(x - 2)\\ = \left[ {(x + 3).(x - 1)} \right].(x - 2)\\ = (x.x - 1.x + 3.x - 3.1)(x - 2)\\ = ({x^2} + 2x - 3)(x - 2)\\ = {x^2}.x - 2.{x^2} + 2x.x - 2x.2 - 3.x + 3.2\\ = {x^3} - 7x + 6\end{array}\)
(Trả lời bởi Hà Quang Minh)
Hoạt động 2 (SGK Chân trời sáng tạo trang 38,39)
Thực hiện phép nhân \((3x + 1)({x^2} - 2x + 1)\), rồi đoán xem \((3{x^3} - 5{x^2} + x + 1):(3x + 1)\) bằng đa thức nào.
Thảo luận (1)Hướng dẫn giải\(\begin{array}{l}(3x + 1)({x^2} - 2x + 1)\\ = 3x({x^2} - 2x + 1) + 1({x^2} - 2x + 1)\\ = 3{x^3} - 6{x^2} + 3x + {x^2} - 2x + 1\\ = 3{x^3} - 5{x^2} + x + 1\end{array}\)
Vì \((3x + 1)({x^2} - 2x + 1) = 3{x^3} - 5{x^2} + x + 1\)
\( \Rightarrow (3{x^3} - 5{x^2} + x + 1):(3x + 1) = {x^2} - 2x + 1\)
(Trả lời bởi Hà Quang Minh)
Thực hành 2 (SGK Chân trời sáng tạo trang 38,39)
Thực hiện phép chia P(x) = \((6{x^2} + 4x)\) cho Q(x) = 2x.
Thảo luận (1)Hướng dẫn giải
Vận dụng 2 (SGK Chân trời sáng tạo trang 38,39)
Thực hiện các phép chia sau \(\frac{{9{x^2} + 5x + x}}{{3x}}\) và \(\frac{{(2{x^2} - 4x) + (x - 2)}}{{2 - x}}\)
Thảo luận (1)Hướng dẫn giải\(\frac{{9{x^2} + 5x + x}}{{3x}} = \frac{{9{x^2} + 6x}}{{3x}} = \frac{{9{x^2}}}{{3x}} + \frac{{6x}}{{3x}} = 3x + 2\)
\(\frac{{2{x^2} - 3x - 2}}{{2 - x}} = \frac{{2{x^2} - 3x - 2}}{{ - x + 2}} = - 2x - 1\)
(Trả lời bởi Hà Quang Minh)
Thực hành 3 (SGK Chân trời sáng tạo trang 38,39)
Thực hiện phép chia \(({x^2} + 5x + 9):(x + 2)\)
Thảo luận (1)Hướng dẫn giải
Vận dụng 3 (SGK Chân trời sáng tạo trang 38,39)
Tính diện tích đáy của một hình hộp chữ nhật (Hình 3) có chiều cao bằng (x + 3) cm và có thể tích bằng \(({x^3} + 8{x^2} + 19x + 12)\)\(c{m^3}\)
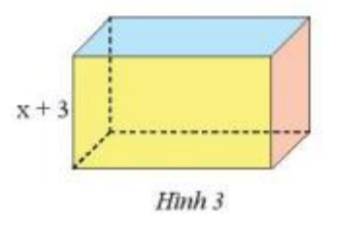
Thảo luận (1)Hướng dẫn giảiTham khảo:
\( \Rightarrow ({x^3} + 8{x^2} + 19x + 12):(x + 3) =\) diện tích đáy
Ta có :
Vậy diện tích đáy là : \({x^2} + 5x + 4\) \(c{m^2}\)
(Trả lời bởi Kiều Sơn Tùng)
Thực hành 4 (SGK Chân trời sáng tạo trang 40)
Thực hiện phép tính \(\dfrac{1}{5}.({x^2} + 1).5\)
Thảo luận (1)Hướng dẫn giải\(\dfrac{1}{5}({x^2} + 1).5 \\= \dfrac{1}{5}.5.({x^2} + 1) \\= (\dfrac{1}{5}.5).{x^2} + 1\\ = 1. ({x^2} + 1)\\= {x^2} + 1\)
(Trả lời bởi Hà Quang Minh)
Bài 1 (SGK Chân trời sáng tạo trang 40)
Thực hiện phép nhân.
a) \((4x - 3)(x + 2)\)
b) \((5x + 2)( - {x^2} + 3x + 1)\)
c) \((2{x^2} - 7x + 4)( - 3{x^2} + 6x + 5)\)
Thảo luận (1)Hướng dẫn giảia) \(\begin{array}{l}(4x - 3)(x + 2) = 4x(x + 2) - 3(x + 2)\\ = 4{x^2} + 8x - 3x - 6\end{array}\)
\( = 4{x^2} + 5x - 6\)
b) \((5x + 2)( - {x^2} + 3x + 1)\)
\( = 5x( - {x^2} + 3x + 1) + 2( - {x^2} + 3x + 1)\)
\( = - 5{x^3} + 15{x^2} + 5x - 2{x^2} + 6x + 2\)
\( = - 5{x^3} + 13{x^2} + 11x + 2\)
c) \((2{x^2} - 7x + 4)( - 3{x^2} + 6x + 5)\)
\( = 2{x^2}( - 3{x^2} + 6x + 5) - 7x( - 3{x^2} + 6x + 5) + 4( - 3{x^2} + 6x + 5)\)
\( = 2{x^2}( - 3{x^2}) + 2{x^2}.6x + 2{x^2}.5 + 7x.3{x^2} - 7x.6x - 7x.5 + 4( - 3{x^2}) + 4.6x + 4.5\)
\(= - 6{x^4} + 33{x^3} - 44{x^2} - 11x + 20\)
(Trả lời bởi Hà Quang Minh)