Bài 4. Hình quạt tròn và hình vành khuyên

Hướng dẫn giải

a) Ta có độ dài của toàn bộ hàng rào là:

C = 2\(\pi \)R = 2.\(\pi \).10 = 20\(\pi \) m

b) Độ dài của mỗi phần hàng rào là:

\(\frac{C}{{360}} = \frac{{20\pi }}{{360}} = \frac{\pi }{{18}}\) m

c) Độ dài của n phần hàng rào là: n.\(\frac{\pi }{{18}}\) m.

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Cung 72^o , bán kính R = 25 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .25.72}}{{180}} \approx 31,42\)cm.

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Ta có độ dài cung AB = \(\widehat {AOB} = {80^o}\), bán kính R = 10 m có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .10.80}}{{180}} \approx 13,96\) (m)

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

a) Ta có thể tính diện tích của miếng pizza trong Hình 4a theo góc ở tâm và bán kính của ổ bánh.

b) i) Chia một hình tròn bán kính R thành 360 phần bằng nhau, diện tích mỗi phần đó là: \(\frac{{\pi {R^2}}}{{360}}\).

ii) diện tích phần hình tròn ghép bởi n phần bằng nhau là: \(n.\frac{{\pi {R^2}}}{{360}}\)

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Hình quạt tròn với bán kính R = 20 cm, ứng với cung 72^o có diện tích là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.20}^2}.72}}{{360}} \approx 251,33\)(cm²)

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Ta có độ dài cung AB = \(\widehat {AOB} = {55^o}\), bán kính R = 15 m có độ dài là:

\(S = \frac{{\pi {R^2}n}}{{360}} = \frac{{\pi {{.15}^2}.55}}{{360}} \approx 108\) cm².

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

a) Ta có hình vẽ:

b) Diện tích S của (C) là: \(S = 5^2\pi  = 25\pi \approx 78,54 (cm^2)\)

Diện tích S’ của (C’) là \(S’ = 8^2\pi = 64\pi \approx 201,06 (cm^2)\)

c) Hiệu số (S’ – S) biểu diễn diện tích của phần tô màu xanh đậm trong hình 9.

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Diện tích hình vành khuyên giới hạn bởi hai đường tròn (O; 10 cm) và (O; 20 cm) là:

\(S = \pi ({R^2} - {r^2}) = \pi ({20^2} - {10^2}) = 300\pi  \approx 942,48\) cm².

(Trả lời bởi Nguyễn Quốc Đạt)

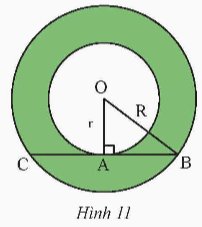
Hướng dẫn giải

a) Vì BC là tiếp tuyến của đường tròn (O; r) tại A nên OA \( \bot \)BC

Xét tam giác OAB vuông tại A , ta có:

AB = \(\sqrt {O{B^2} - O{A^2}}  = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)

Tương tự với tam giác OCA vuông tại A, ta có

AC = \(\sqrt {O{C^2} - O{A^2}}  = \sqrt {{R^2} - {r^2}} \) (theo định lý Pythagore)

Vậy BC = AB + AC = 2\(\sqrt {{R^2} - {r^2}} \).

b) Ta có BC = 2\(\sqrt {{R^2} - {r^2}} \) = \(a\sqrt 3 \) suy ra \(\sqrt {{R^2} - {r^2}} \) = \(\frac{{a\sqrt 3 }}{2}\)

Diện tích hình khuyên giới hạn bởi hai đường tròn (O; r) và (O; R) theo a là:

\(S = \pi ({R^2} - {r^2})\) = \(\pi {\left( {\frac{{a\sqrt 3 }}{2}} \right)^2} = \frac{{3\pi }}{4}{a^2}\).

(Trả lời bởi Nguyễn Quốc Đạt)

Hướng dẫn giải

Ta có độ dài cung \({30^o}\), bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.30}}{{180}} = \pi \approx 3,14 (cm)\)

Ta có độ dài cung \({90^o}\), bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.90}}{{180}} = 3\pi \approx 9,42 (cm)\)

Ta có độ dài cung \({120^o}\), bán kính R = 6 cm có độ dài là:

\(l = \frac{{\pi Rn}}{{180}} = \frac{{\pi .6.120}}{{180}} = 4\pi \approx 12,57 (cm)\)

(Trả lời bởi Nguyễn Quốc Đạt)