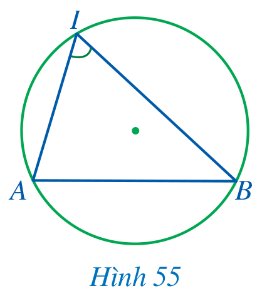
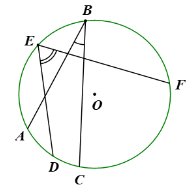
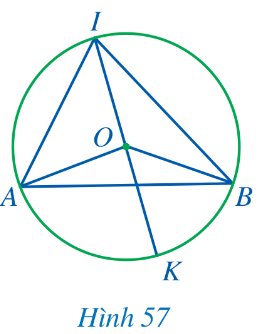
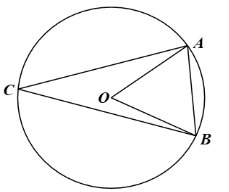
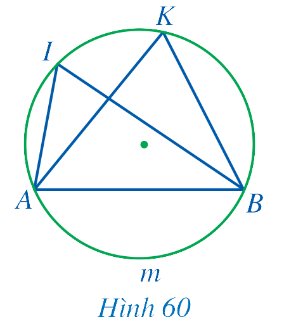
Bác Ngọc dự định làm khung sắt cho khuôn cửa sổ ngôi nhà có dạng đường tròn như Hình 44. Hai thanh chắn cửa sổ gợi nên một góc có đỉnh thuộc đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.

Góc có đặc điểm như vậy trong toán học gọi là góc gì?