Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là \(828m^2\) ?
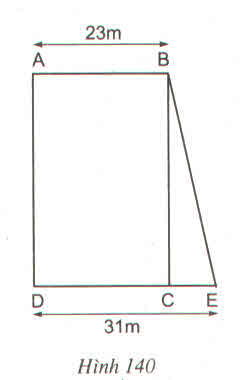
Tính diện tích mảnh đất hình thang ABED theo các độ dài đã cho trên hình 140 và biết diện tích hình chữ nhật ABCD là \(828m^2\) ?

Vì sao hình chữ nhật ABCD và hình bình hành ABEF (h.141) lại có cùng diện tích ? Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước ?

Thảo luận (2)Hướng dẫn giải
Hình chữ nhật ABCD và hình bình hành ABEF có đáy chung là AB và có chiều cao bằng nhau, vậy chúng có diện tích bằng nhau.
Suy ra cách vẽ một hình chữ nhật có cùng diện tích với một hình bình hành cho trước:
- Lấy nột cạnh của hình bình hành ABEF làm một cạnh của hình chữ nhật cần vẽ, chẳng hạn cạnh AB.
- Vẽ đường thẳng EF.
- Từ A và b vẽ các đường thẳng vuông góc với đường thẳng EF, chúng cắt đường thẳng EF lần lượt tại D, C. vẽ các đoạn thẳng AD, BC. ABCD là hình chữ nhật có cùng diện tích với hình bình hành ABEF đã cho
(Trả lời bởi Nhật Linh)
Xem hình 142 (IG //FU). Hãy đọc tên một số hình có cùng diện tích với hình bình hành FIGE ?
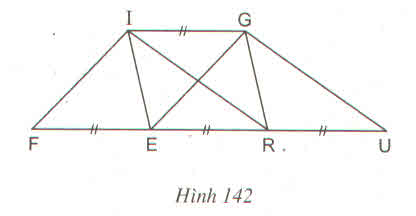
Thảo luận (2)Hướng dẫn giảiTa có IG // FU nên khoảng cách giữa hai đường thẳng IG và FU không đổi và bằng h. Các hình bình hành FIGE, IGRE, IGUR có cạnh bằng nhau FE = ER = RU có cùng chiều cao ứng với cạnh đó nên diện tích chúng bằng nhau. Tức là SFIGR = SIGRE = SIGUR( = h. FE)
Mặt khác các tam giác IFG, GEU có cạnh đáy FR và EU bằng nhau, bằng hai lần cạnh hình bình hành FIGE nên diện tích chúng bằng nhau:
SIFR = SGEU = SFIGE
Vậy SFIGE = SIGRE = SIGUR = SIFR = SGEU
(Trả lời bởi Tuyết Nhi Melody)
Khi nối trung điểm của hai đáy hình thang, tại sao ta được hai hình thang có diện tích bằng nhau ?
Thảo luận (1)Hướng dẫn giảiCho hình thang ABCD. Gọi M, N lần lượt là trung điểm của hay đáy AB, CD. Ta có hai hình thang AMND và BMNC có cùng chiều cao, có đáy trên bằng nhau AM = MB, có đáy dưới bằng nhau DN = NC. Vậy chúng có diện tích bằng nhau.
(Trả lời bởi Tuyết Nhi Melody)
Trên hình 143 ta có hình thang ABCD với đường trung bình EF và hình chữ nhật. Hãy so sánh diện tích hai hình này, từ đó suy ra một cách chứng minh khác về công thức diện tích hình thang ?

Thảo luận (2)Hướng dẫn giảiTa có hình thang ABCD ( AB// CD), với đường trung bình EF và hình chữ nhật GHIK như hình vẽ .
Dễ dàng chứng minh
∆AEG = ∆DEK;
∆BFH = ∆CFI
Do đó SABCD = SAEKIFB + SDEK + SCFI = SAEKIFB + SAEG + SBFH = SGHIK
Nên
SABCD = SGHIK = EF. AJ mà EF =
Do đó SABCD =
Vậy ta gặp lại công thức tính diện tích hình thang đã được học nhưng bằng một phương pháp chứng minh khác. Mặt khác, ta phát hiện công thức mới : Diện tích hình thang bằng tích của đường trung bình hình thang với chiều cao.
(Trả lời bởi Tuyết Nhi Melody)
Xem hình 144. Hãy chỉ các hình có cùng diện tích (lấy ô vuông làm đơn vị diện tích)
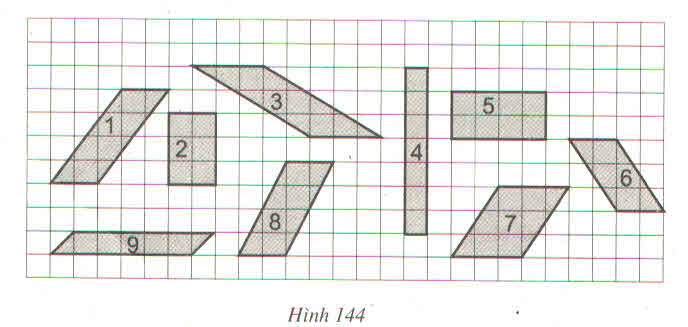
Thảo luận (2)Hướng dẫn giảiCác hình 2,6,9 có cùng diện tích là 6 ô vuông.
Các hình 1, 5, 8 có cùng diện tích là 8 ô vuông.
Các hình 3,7 có cùng diện tích là 8 ô vuông.
Hình 4 có diện tích là 7 ô vuông nên không có diện tích với một trong các hình đã cho.
(Trả lời bởi Tuyết Nhi Melody)
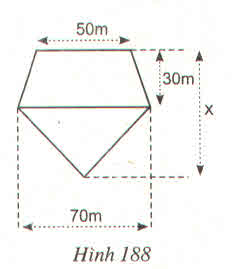
Tính x, biết đa giác ở hình 188 có diện tích là \(3375m^2\)
Thảo luận (1)Hướng dẫn giải
Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có cạnh AB = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được bao nhiêu hình ABEF như vậy ?
Thảo luận (2)Hướng dẫn giải
Cho hình chữ nhật ABCD có cạnh AB = 5cm, BC = 3cm. Vẽ hình bình hành ABEF có các cạnh AB = 5cm, BE = 5cm và có diện tích bằng diện tích của hình chữ nhật ABCD. Vẽ được mấy hình ABEF như vậy ?
Thảo luận (1)Hướng dẫn giải
Tính diện tích của một hình thang vuông, biết hai đáy có độ dài 2cm và 4cm, góc tạo bởi một cạnh bên và đáy lớn có số đo bằng \(45^0\)
Thảo luận (2)Hướng dẫn giải
Hạ đường cao CE thì EB = AB - AE = AB - DC = 4 - 2 =2.
Tam giác vuông EBC có góc B = 45 độ nên nó là tam giác vuông cân. Suy ra CE = EB = 2.
\(dt\left(ABCD\right)=\dfrac{AB+CD}{2}.CE=\dfrac{4+2}{2}.2=6\left(cm^2\right)\)
(Trả lời bởi Giáo viên Toán)