Quan sát máy cắt sắt đang hoạt động (Hình 32), ta thấy các mảnh vụn sắt chuyển động và văng ra theo phương tiếp tuyến với đường tròn mép đĩa cắt.

Tiếp tuyến của đường tròn có tính chất và được nhận biết như thế nào?
Quan sát máy cắt sắt đang hoạt động (Hình 32), ta thấy các mảnh vụn sắt chuyển động và văng ra theo phương tiếp tuyến với đường tròn mép đĩa cắt.

Tiếp tuyến của đường tròn có tính chất và được nhận biết như thế nào?
Cho đường thẳng a là tiếp tuyến của đường tròn (O; R). Gọi H là hình chiếu của tâm O trên đường thẳng a (Hình 33).
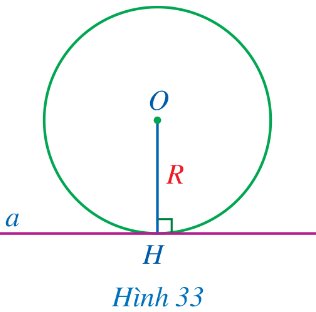
a) So sánh khoảng cách OH từ tâm O đến đường thẳng a và bán kính R.
b) Điểm H có thuộc đường tròn (O; R) hay không?
c) Điểm H có phải là tiếp điểm của đường thẳng a và đường tròn (O; R) hay không?
d) Đường thẳng a có vuông góc với bán kính đi qua tiếp điểm hay không?
Thảo luận (1)Hướng dẫn giảia) \(OH = R\).
b) Điểm \(H\) có thuộc đường tròn \(\left( {O;R} \right)\).
c) Điểm \(H\) là tiếp điểm của đường thẳng \(a\) và đường tròn \(\left( {O;R} \right)\).
d) Đường thẳng \(a\) có vuông góc với bán kính đi qua tiếp điểm.
(Trả lời bởi datcoder)
Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C. Đường tròn (O) tiếp xúc với đường thẳng AB tại điểm C. Chứng minh AO2 + BC2 = BO2 + AC2.
Thảo luận (1)Hướng dẫn giải
Vì đường thẳng \(AB\) tiếp xúc với đường tròn \(\left( O \right)\) tại \(C\) nên \(OC \bot AB\). Suy ra tam giác \(OBC\) vuông tại \(C\), tam giác \(OAC\) vuông tại C.
Áp dụng định lý Pythagore vào tam giác \(OAC\) vuông tại \(C\), ta có:
\(O{A^2} = O{C^2} + A{C^2} \Rightarrow O{C^2} = O{A^2} - A{C^2}\,\,\left( 1 \right)\).
Áp dụng định lý Pythagore vào tam giác \(OBC\) vuông tại \(C\), ta có:
\(O{B^2} = O{C^2} + B{C^2} \Rightarrow O{C^2} = O{B^2} - B{C^2}\,\,\,\left( 2 \right)\).
Từ (1) và (2) suy ra \(O{A^2} - A{C^2} = O{B^2} - B{C^2} \Rightarrow O{A^2} + B{C^2} = O{B^2} + A{C^2}\).
(Trả lời bởi datcoder)
Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a ⊥ OH (Hình 35).
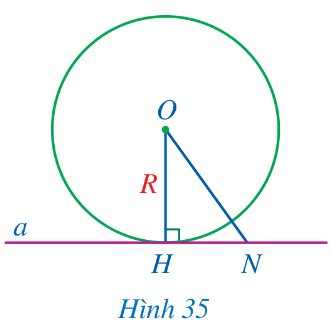
a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.
b) Giả sử N là điểm thuộc đường thẳng a và N khác H. So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?
c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?
Thảo luận (1)Hướng dẫn giảia) Khoảng cách từ điểm \(O\) đến đường thẳng \(a\) là đoạn \(OH\).
Do điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OH = R\).
Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(a\) bằng bán kính \(R\).
b) Xét tam giác \(OHN\) vuông tại \(H\) có: \(ON\) là cạnh huyền, \(OH\) là cạnh góc vuông.
Suy ra \(ON > OH\), lại có \(OH = R\). Vậy \(ON > R\).
Điểm \(N\) không thuộc đường tròn \(\left( {O;R} \right)\).
c) Đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\).
(Trả lời bởi datcoder)
Cho đường tròn (O; R) và (O’; R’) tiếp xúc ngoài nhau tại điểm I. Gọi d là tiếp tuyến của (O; R) tại điểm I. Chứng minh d là tiếp tuyến của (O’; R’).
Thảo luận (1)Hướng dẫn giải
Vì (O;R) và (O'R') tiếp xúc ngoài nhau tại I nên O, I, O' thẳng hàng và I nằm giữa O và O'.
Do \(d\) là tiếp tuyến của \(\left( {O;R} \right)\) tại điểm \(I\) nên \(OI \bot d\) hay \(O'I \bot d\).
Mà \(I \in \left( {O'} \right),I \in d\) nên \(d\) là tiếp tuyến của \(\left( {O'R'} \right)\).
(Trả lời bởi datcoder)
Cho hai đường tròn (O), (O’) cắt nhau tại hai điểm A, B sao cho đường thẳng OA là tiếp tuyến của đường tròn (O’). Chứng minh đường thẳng O’B là tiếp tuyến của đường tròn (O).
Thảo luận (1)Hướng dẫn giải
Do \(OA\) là tiếp tuyến của đường tròn \(\left( {O'} \right)\) nên \(O'A \bot OA\). Vậy \(\widehat {OAO'} = 90^\circ \).
Xét tam giác \(OAO'\) và tam giác \(OBO'\) có:
\(\left\{ \begin{array}{l}O'A = O'B\\OO'\,\,chung\\OA = OB\end{array} \right.\)
\(\begin{array}{l} \Rightarrow \Delta OAO' = \Delta OBO'\left( {c.c.c} \right)\\ \Rightarrow \widehat {OAO'} = \widehat {OBO'}\end{array}\).
Mà \(\widehat {OAO'} = 90^\circ \) nên \(\widehat {OBO'} = 90^\circ \) hay \(OB \bot O'B\).
Vậy đường thẳng \(O'B\) là tiếp tuyến của đường tròn \(\left( O \right)\).
(Trả lời bởi datcoder)
Cho đường tròn (O; R). Các đường thẳng c, d lần lượt tiếp xúc với đường tròn (O; R) tại A, B và cắt nhau tại M (Hình 38).
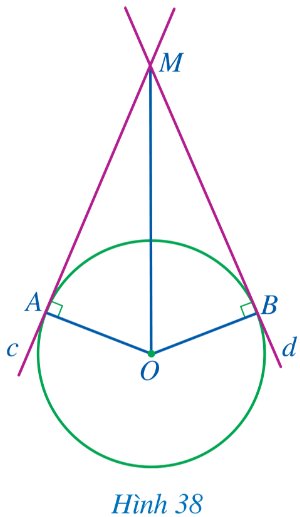
a) Các tam giác MOA và MOB có bằng nhau hay không?
b) Hai đoạn thẳng MA và MB có bằng nhau hay không?
c) Tia MO có phải là tia phân giác của góc AMB hay không?
d) Tia OM có phải tia phân giác của góc AOB hay không?
Thảo luận (1)Hướng dẫn giảia) Do \(MA\) là tiếp tuyến của \(\left( {O;R} \right)\) nên \(MA \bot AO\) suy ra \(\widehat {MAO} = 90^\circ \).
Do \(MB\) là tiếp tuyến của \(\left( {O;R} \right)\) nên \(MB \bot BO\) suy ra \(\widehat {MBO} = 90^\circ \).
Xét tam giác \(MOA\)và tam giác \(MOB\) có:
\(\widehat {MAO} = \widehat {MBO} = 90^\circ \)
\(OA = OB = R\)
\(OM\) chung
\( \Rightarrow \Delta MOA = \Delta MOB\) (cạnh huyền – cạnh góc vuông).
b) Do \(\Delta MOA = \Delta MOB\) nên \(MA = MB\) (2 cạnh tương ứng).
c) Do \(\Delta MOA = \Delta MOB\) nên \(\widehat {AMO} = \widehat {BMO}\) (2 góc tương ứng) suy ra \(MO\) là tia phân giác của góc \(AMB\).
d) Do \(\Delta MOA = \Delta MOB\) nên \(\widehat {MOA} = \widehat {MOB}\) (2 góc tương ứng) suy ra \(OM\) là tia phân giác của góc \(AOB\).
(Trả lời bởi datcoder)
Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn. Hai đường thẳng c, d qua M lần lượt tiếp xúc với (O) tại A, B. Biết \(\widehat{AMB}\) = 120°. Chứng minh AB = R.
Thảo luận (1)Hướng dẫn giải
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên MO là tia phân giác của góc AMB, suy ra \(\widehat {AMO} = \widehat {BMO} = \frac{{\widehat {AMB}}}{2} = 60^\circ \).
Xét tam giác \(AMO\) vuông tại \(A\) có:
\(\widehat {AMO} + \widehat {MOA} = 90 \\60^\circ + \widehat {MOA} = 90^\circ \\ \widehat {MOA} = 30^\circ \)
Vì \(MA,MB\) là các tiếp tuyến của \(\left( O \right)\) nên OM là tia phân giác của góc AOB, suy ra \(\widehat {AOB} = 2\widehat {AOM} = 2.30^\circ = 60^\circ \).
Xét tam giác \(AOB\) có: \(OA = OB = R\) nên tam giác \(AOB\) cân tại \(O\).
Lại có \(\widehat {AOB} = 60^\circ \) suy ra tam giác \(AOB\) là tam giác đều.
Vậy \(AO = OB = AB = R\).
(Trả lời bởi datcoder)
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.
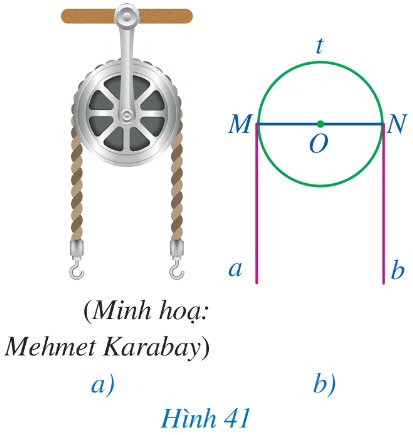
Giả sử ròng rọc được minh họa bởi đường tròn (O), sợi dây vắt qua ròng rọc được minh họa bởi nửa đường tròn MtN và hai tiếp tuyến Ma, Nb của đường tròn (O) (Hình 41b). Chứng minh Ma // Nb.
Thảo luận (1)Hướng dẫn giảiDo \(Ma\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(Ma \bot OM\) hay \(Ma \bot MN\).
Do \(Nb\) là tiếp tuyến của đường tròn \(\left( O \right)\) nên \(Nb \bot ON\) hay \(Nb \bot MN\).
Từ đó suy ra \(Ma//Nb\) (quan hệ từ vuông góc tới song song).
(Trả lời bởi datcoder)
Cho đường tròn (O) và dây AB. Điểm M nằm ngoài đường tròn (O) thỏa mãn điểm B nằm trong góc MAO và \(\widehat{MAB}=\dfrac{1}{2}\widehat{AOB}\). Chứng minh đường thẳng MA là tiếp tuyến của đường tròn (O).
Thảo luận (1)Hướng dẫn giải
Ta có: \(OA = OB = R\) nên tam giác \(OAB\) cân tại \(O\) suy ra \(\widehat {OAB} = \widehat {OBA}\).
Xét tam giác \(OAB\) cân tại \(O\) có:
\(\begin{array}{l}\widehat {OAB} + \widehat {OBA} + \widehat {AOB} = 180^\circ \Rightarrow \widehat {OAB} + \widehat {OAB} + \widehat {AOB} = 180^\circ \\ \Rightarrow 2\widehat {OAB} = 180^\circ - \widehat {AOB} \Rightarrow \widehat {OAB} = 90^\circ - \frac{1}{2}\widehat {AOB}.\end{array}\)
Ta có: \(\widehat {OAM} = \widehat {OAB} + \widehat {BAM} = 90^\circ - \frac{1}{2}\widehat {AOB} + \frac{1}{2}\widehat {AOB} = 90^\circ .\)
Suy ra \(OA \bot AM\). Vậy \(MA\) là tiếp tuyến của đường tròn \(\left( O \right)\).
(Trả lời bởi datcoder)