Cho đường thẳng a và đường tròn (O; R) thỏa mãn đường thẳng a đi qua điểm H thuộc đường tròn (O; R) và a ⊥ OH (Hình 35).
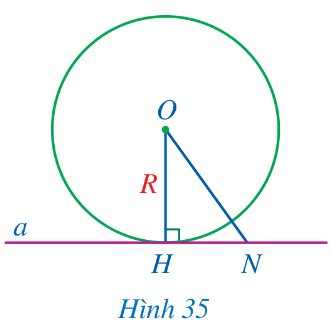
a) So sánh khoảng cách từ điểm O đến đường thẳng a và bán kính R.
b) Giả sử N là điểm thuộc đường thẳng a và N khác H. So sánh ON và R. Điểm N có thuộc đường tròn (O; R) hay không?
c) Đường thẳng a có phải là tiếp tuyến của đường tròn (O; R) hay không?
a) Khoảng cách từ điểm \(O\) đến đường thẳng \(a\) là đoạn \(OH\).
Do điểm \(H\) thuộc đường tròn \(\left( {O;R} \right)\) nên \(OH = R\).
Vậy khoảng cách từ điểm \(O\) đến đường thẳng \(a\) bằng bán kính \(R\).
b) Xét tam giác \(OHN\) vuông tại \(H\) có: \(ON\) là cạnh huyền, \(OH\) là cạnh góc vuông.
Suy ra \(ON > OH\), lại có \(OH = R\). Vậy \(ON > R\).
Điểm \(N\) không thuộc đường tròn \(\left( {O;R} \right)\).
c) Đường thẳng \(a\) là tiếp tuyến của đường tròn \(\left( {O;R} \right)\).


