Tính thể tích khối tứ diện đều cạnh a ?
Bài 3: Khái niệm về thể tích của khối đa diện
Bài 1 (SGK trang 25)
Thảo luận (1)
Bài 2 (SGK trang 25)
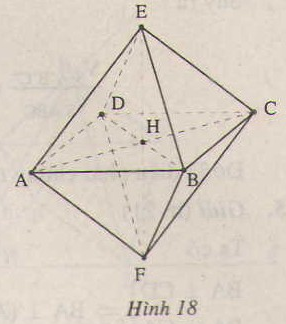
Tính thể tích khối đa diện đều cạnh a ?
Thảo luận (1)Hướng dẫn giảiChia khối tám mặt đều cạnh a thành hai khối chóp tứ giác đều cạnh a.
Gọi h là chiều cao của khối chóp thì dễ thấy
h2=a2−(√22)2=a22h2=a2−(22)2=a22 nên h=a√22h=a22
Từ đó thể tích khối tám mặt đều cạnh a là:
V=2.13.√22.a2=a3√23V=2.13.22.a2=a323.
(Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...)
Bài 3 (SGK trang 25)
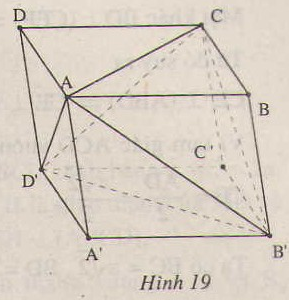
Cho hình hộp ABCD.A'B'C'D'. Tính tỉ số thể tích khối hộp đó và thể tích của khối tứ diện ACB'D' ?
Thảo luận (1)Hướng dẫn giảiGọi S là diện tích đáy ABCD và h là chiều cao của khối hộp. Chia khối hộp thành khối tứ diện ACB’D’ và bốn khối chóp A.A’B’D’, C.C’B’D’, B’.BAC và D’. DAC. Ta thấy bốn khối chóp sau đều có diện tích đáy bằng
và chiều cao bằng h, nên tổng các thể tích của chúng bằng
.
Từ đó suy ra thể tích của khối tứ diện
ACB’D’=
. Do đó tỉ số của thể tích khối hộp đó và thể tích của khối tứ diện ACB’D’ bằng 3.
(Trả lời bởi Võ Đông Anh Tuấn)
Bài 4 (SGK trang 25)
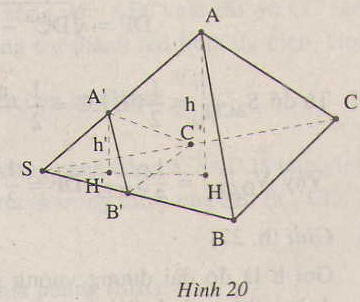
Cho hình chóp S.ABC. Trên các đoạn thẳng SABC. Trên các đoạn thẳng SA, SB, SC lần lượt lấy ba điểm A', B', C' khác với S. Chứng minh rằng :
\(\dfrac{V_{S.A'B'C'}}{V_{S.ABC}}=\dfrac{SA'}{SA}.\dfrac{SB'}{SB}.\dfrac{SC'}{SC}\)
Thảo luận (1)Hướng dẫn giảiGọi h và h’ lần lượt là chiều cao hạ từ A, A’ đến mặt phẳng (SBC).
Gọi S1 và S2 theo thứ tự là diện tích các tam giác SBC và SB’C’.
Khi đó ta có h′h=SA′SAh′h=SA′SA và 12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC12B′SC′.SB′.SC′12BSC.SB.SC=SB′SB.SC′SC
Suy ra VS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SCVS.A′B′C′VS.ABC=VA′.SB′C′VA.SBC=13h′S213hS1=SA′SA⋅SB′SB⋅SC′SC
Đó là điều phải chứng minh.
(Trả lời bởi ¨°o.O♫♀¤♪ Zin Phan ♪¤♂♫O...)
Bài 5 (SGK trang 26)
Cho tam giác ABC vuông cân ở A và AB = a. Trên đường thẳng đi qua C và vuông góc với mặt phẳng (ABC) lấy điểm D sao cho CD = a. Mặt phẳng qua C vuông góc với DB, cắt BD tại F và cắt AD tại E. Tính thể tích khối tứ diện CDEF theo a ?
Thảo luận (1)Hướng dẫn giảigọi (α) là mặt phẳng qua C vuông góc với BD
(Trả lời bởi _silverlining)
tam giác ABC vuông cân ở A và AB= a => BC = a√2
tam giác ACD vuông cân ở C và AC = a => AD = a√2
BD^2 = CD^2 + BC^2 = a^2 + 2a^2 = 3a^2 => BD = a√3
BD L (α) => BD L CF
DC L (ABC) => DC L BC
ta có:
CD^2 = DF.BD => DF = CD^2/BD = a^2/(a√3) = a/√3
BD L (α) => BD L EF
DC L (ABC) và AB L AC => AB L AD ( định lý 3 đường vuông góc)
=> ΔDEF ~ Δ DBA => DF/DA = DE/BD
=> DE = DF.BD/DA = (a/√3)(a√3)/(a√2) = a/√2
V = V(DABC) = S(ABC).CD/3 = (a^2/2).a/3 = a^3/6
V1 = V(CDEF) = V(DCEF)
ta có:
V1/V = (DC/DC).(DE/DA).(DF/DB) = 1.[(a/√2)/(a√2)].[(a/√3)/(a√3)] = 1/6
=> V1 = V/6 = (a^3/36)
Bài 6 (SGK trang 26)
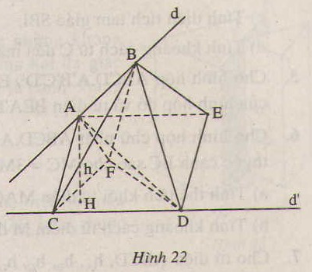
Cho hai đường thẳng chéo nhau d và d'. Đoạn thẳng AB có độ dài a trượt trên d, đoạn thẳng CD có độ dài b trượt trên d'. Chứng minh rằng khối tứ diện ABCD có thể tích không đổi ?
Thảo luận (1)Hướng dẫn giảiGọi h là độ dài đường vuông góc chung của d và d’, α là góc giữa hai đường thẳng d và d’. Qua B, A, C dựng hình bình hành BACF. Qua A,C, D dựng hình bình hành ACDE.
Khi đó CFD.ABE là một hình lăng trụ tam giác. Ta có:
VDABC=VDFCB=VBCDF
=
VCFD.ABE
=
hSFCD=
h.
ab. sinα
=
h. ab. sinα (là một số không đổi).
(Trả lời bởi _silverlining)
Xem thêm tại: http://loigiaihay.com/cau-6-trang-26-sgk-hinh-hoc-12-c47a2782.html#ixzz4cxsiVwHA
Bài 1.10 (Sách bài tập trang 20)
Cho khối chóp tam giác đều S.ABC có đáy là tam giác đều cạnh a, các cạnh bên tạo với đáy một góc \(60^0\). Hãy tính thể tích của khối chóp đó ?
Thảo luận (1)Hướng dẫn giải
Bài 1.11 (Sách bài tập trang 20)
Cho khối chóp S.ABC có đáy là tam giác cân, AB = AC=5a; BC = 6a và các mặt bên tạo với đáy một góc \(60^0\). Hãy tính thể tích của khối chóp đó ?
Thảo luận (1)Hướng dẫn giải
Bài 1.12 (Sách bài tập trang 20)
Cho hình chóp tam giác S.ABC có đáy là tam giác vuông ở B. Cạnh SA vuông góc với đáy. Từ A kẻ các đoạn thẳng AD vuông góc với SB và AE vuông góc với SC. Biết rằng AB = a, BC = b, SA = c
a) Hãy tính thể tích khối chóp S.ADE
b) Tính khoảng cách từ E đến mặt phẳng (SAB)
Thảo luận (1)Hướng dẫn giải
Bài 1.13 (Sách bài tập trang 20)
Chứng minh rằng tổng các khoảng cách từ một điểm trong bất kì một tứ diện đều đến các mặt của nó là một số không đổi ?
Thảo luận (1)Hướng dẫn giải