Cắt bìa theo mẫu dưới đây (h.1.23), gấp theo đường kẻ, rồi dán các mép lại để được các hình tứ diện đều, hình lập hương và hình bát diện đều ?
Bài 2: Khối đa diện lồi và khối đa diện đều
Bài 1 (SGK trang 18)
Thảo luận (1)
Bài 2 (SGK trang 18)
Cho hình lập phương (H). Gọi (H') là hình bát diện đều có các đỉnh là tâm các mặt của (H). Tính tỉ số diện tích toàn phần của (H) và (H') ?
Thảo luận (1)Hướng dẫn giảiCho hình lập phương ABCD.A’B’C’D’ . Gọi E, F, G, I, J, K là tâm của các mặt của nó. Khi đó các đỉnh E, F, G, I, J, K tạo thành hình bát diện đều EFGIJK.
Đặt AB = a, thì
Diện tích tam giác đều (EFJ) bằng
.
Suy ra diện tích toàn phần của hình bát diện (H’) bằng
. Diện tích toàn phần của hình lập phương (H) bằng
. Do đó tỉ số diện tích toàn phần của (H) và (H') bằng
(Trả lời bởi _silverlining)
.
Bài 3 (SGK trang 18)
Chứng minh rằng tâm của các mặt của các hình tứ diện đều là các đỉnh của một hình tứ diện đều ?
Thảo luận (1)Hướng dẫn giảiCho hình tứ diện đều ABCD, cạnh bằng a. Gọi E, F, I, J lần lượt là tâm của các mặt ABC, ABD, ACD, BCD (H.11).
Vì
, nên \(\dfrac{EF}{CD}=\dfrac{1}{3}\)
Suy ra
.
Tương tự, các cạnh khác của tứ diện EFIJ đều bằng
.
Do đó tứ diện EFIJ là một tứ diện đều.
(Trả lời bởi Lê Thiên Anh)
Bài 4 (SGK trang 18)
Cho hình bát diện đều ABCDEF (h.1.24)
Chứng minh rằng :
a) Các đoạn thẳng AF, BD và CE đôi một vuông góc với nhau và cắt nhau tại trung điểm mỗi đường
b) ABFD, AEFC và BCDE là những hình vuông
Thảo luận (1)Hướng dẫn giải
a) Do B, C, D, E cách đều A và F nên chúng đồng phẳng (cùng thuộc mặt phẳng trung trực của AF).
Tương tự, A, B, F, D đồng phẳng và A, C, F, E đồng phẳng
Gọi I là giao của (AF) với (BCDE). Khi đó B, I, D là những điểm chung của hai mặt phẳng (BCDE) và (ABFD) nên chúng thẳng hàng. Tương tự, E, I , C thẳng hàng.
Vậy AF, BD, CE đồng quy tại I.
Vì BCDE là hình thoi nên BD vuông góc với BC và cắt BC tại I là trung điểm của mỗi đường. I là trung điểm của AF và AF vuông góc với BD và EC, do đó các đoạn thẳng AF, BD, và CE đôi một vuông góc với nhau cắt nhau tại trung điểm của chúng.
b) Do AI vuông góc (BCDE) và AB = AC =AD = AE nên IB = IC= ID = IE. Từ đó suy ra hình thoi BCDE là hình vuông. Tương tự, ABFD, AEFC là những hình vuông
(Trả lời bởi Võ Đông Anh Tuấn)
Bài 1.6 (Sách bài tập trang 14)
Tính sin của góc tạo bởi hai mặt kề (tức là hai mặt có một cạnh chung) của một tứ diện đều ?
Thảo luận (1)Hướng dẫn giảiCho tứ diện đều ABCD cạnh bằng a. Gọi M và N theo thứ tự là trung điểm của AB và CD. Khi đó góc giữa hai mặt (CAB) và (DAB) bằng \(\widehat{CMD}=2\widehat{CMN}\)
Ta có :
\(CM=\dfrac{a\sqrt{3}}{2};CN=\dfrac{a}{2}\)
Do đó :
\(\sin\widehat{CMN}=\dfrac{\dfrac{a}{2}}{\dfrac{a\sqrt{3}}{2}}=\dfrac{1}{\sqrt{3}}\)
Từ đó suy ra :
\(\sin\widehat{CMD}=\dfrac{2\sqrt{2}}{3}\)
(Trả lời bởi Nguyen Thuy Hoa)
Bài 1.7 (Sách bài tập trang 14)
Cho ba đoạn thẳng bằng nhau, đôi một vuông góc với nhau và cắt nhau tại trung điểm của chúng. Chứng minh rằng các đầu mút của ba đoạn thẳng ấy là các đỉnh của một hình bát diện đều ?
Thảo luận (1)Hướng dẫn giảiGọi độ dài của ba đoạn thẳng đã cho là a. Khi đó các đầu mút của chúng là đỉnh của một hình tám mặt đều, mỗi mặt là tam giác đều có cạnh bằng \(\dfrac{a\sqrt{2}}{2}\)
(Trả lời bởi Nguyen Thuy Hoa)
Bài 1.8 (Sách bài tập trang 14)
Cho một bát diện đều. Hãy chỉ ra một mặt phẳng đối xứng, một tâm đối xứng và một trục đối xứng của nó ?
Thảo luận (1)Hướng dẫn giải
Ta có khối bát diện đều ABCDEF như hình 1.16. Gọi O là giao điểm của EF và (ABCD)
Khi đó mặt phẳng (ABCD), điểm O và đường thẳng EF lần lượt là mặt phẳng đối xứng, tâm đối xứng và trục đối xứng của khối bát diện đều đã cho.
(Trả lời bởi Nguyen Thuy Hoa)
Bài 1.9 (Sách bài tập trang 14)
Cho khối bát diện đều ABCDEF (h.1.9). Gọi O là giao điểm của AC, BD, M và N theo thứ tự là trung điểm của AB và AE. Tính diện tích thiết diện tạo bởi khối bát đó với mặt phẳng (OMN) ?
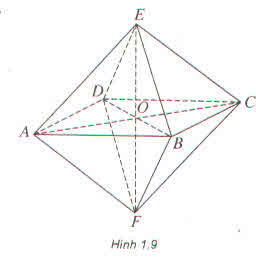
Thảo luận (1)Hướng dẫn giải
Ta có khối bát diện đều ABCDEF, cạnh a. Do MN // (DEBF) nên giao của mặt phẳng (OMN) với mặt phẳng (DEBF) là đường thẳng qua O và song song với MN
Ta nhận thấy đường thẳng này cắt DE và BF tại các trung điểm P và S tương ứng của chúng. Do mặt phẳng (ADE) song song với mặt phẳng (BCF) nên (OMN) cắt (BCF) theo giao tuyến qua S và song song với NP. Dễ thấy giao tuyến này cắt FC tại trung điểm R của nó. Tương tự (OMN) cắt DC tại trung điểm Q của nó. Từ đó suy ra thiết diện tạo bởi hình bát diện đã cho với mặt phẳng (OMN) là lục giác đều có cạnh bằng \(\dfrac{a}{2}\)
Do đó diện tích của nó bằng \(\dfrac{3\sqrt{3}}{8}a^2\)
(Trả lời bởi Nguyen Thuy Hoa)
