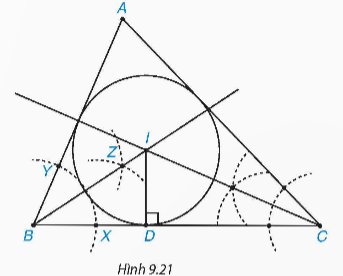
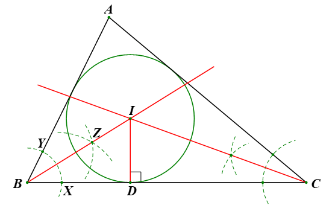
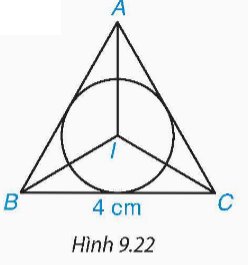
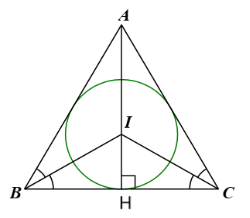
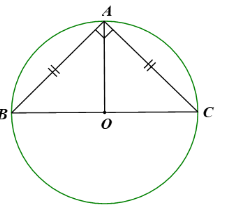
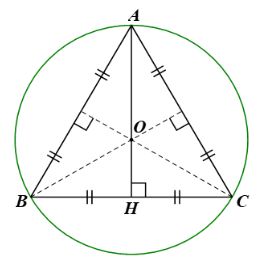
Cho tam giác đều ABC có trọng tâm G.
a) Giải thích vì sao G cũng là tâm đường tròn nội tiếp tam giác ABC.
b) Từ đó, giải thích vì sao bán kính đường tròn nội tiếp tam giác ABC bằng một nửa bán kính đường tròn ngoại tiếp tam giác ABC và bằng \(\dfrac{\sqrt{3}}{6}BC\).
Vẽ đường tròn nội tiếp của tam giác ABC bằng thước kẻ và compa theo các bước sau:
– Vẽ tia phân giác góc B như sau: Dùng compa vẽ một cung tròn tâm B cắt hai cạnh BC, BA lần lượt tại X và Y. Vẽ hai cung tròn tâm X, Y có cùng bán kính, hai cung này cắt nhau tại một điểm Z khác B. Kẻ tia BZ ta được tia phân giác góc B.
– Tương tự, vẽ tia phân giác góc C, cắt tia BZ tại I.
– Vẽ đường cao ID từ I xuống BC (D thuộc BC). Vẽ đường tròn (I; ID) (H.9.21).
Thảo luận (1)Hướng dẫn giải
Cho tam giác đều ABC (H.9.22).
a) Vẽ đường tròn (I; r) nội tiếp tam giác ABC.
b) Biết rằng BC = 4 cm, hãy tính bán kính r.
Thảo luận (1)Hướng dẫn giải
a) Vẽ ba đường phân giác của tam giác ABC. Gọi I là giao điểm của ba đường phân giác đó.
Gọi H là giao điểm của AI và BC. Vẽ đường tròn tâm I, bán kính IH.
Khi đó, đường tròn (I; IH) là đường tròn nội tiếp tam giác ABC cần vẽ.
b) Vì (I; r) nội tiếp tam giác ABC nên bán kính đường tròn nội tiếp tam giác ABC là:
\(r = \frac{{BC\sqrt 3 }}{6} = \frac{{4\sqrt 3 }}{6} = \frac{{2\sqrt 3 }}{3}\left( {cm} \right)\)
(Trả lời bởi datcoder)
Cho đường tròn (O) ngoại tiếp tam giác ABC. Tính bán kính của (O), biết rằng tam giác ABC vuông cân tại A và có cạnh bên bằng \(2\sqrt{2}\) cm.
Thảo luận (1)Hướng dẫn giải
Tam giác ABC vuông cân tại A nên \(AB = AC = 2\sqrt 2 cm\)
Áp dụng định lí Pythagore vào tam giác ABC vuông tại A ta có:
\(B{C^2} = A{B^2} + A{C^2} = {\left( {2\sqrt 2 } \right)^2} + {\left( {2\sqrt 2 } \right)^2} = 16 \Rightarrow BC = 4cm\)
Vì O là trung điểm của BC nên \(OB = OC = \frac{{BC}}{2} = \frac{4}{2} = 2\left( {cm} \right)\)
Vì tam giác ABC vuông tại A nên tam giác ABC nội tiếp đường tròn tâm O, bán kính OC.
Vậy bán kính đường tròn (O) ngoại tiếp tam giác ABC bằng 2cm.
(Trả lời bởi datcoder)
Cho tam giác đều ABC nội tiếp đường tròn (O). Biết rằng đường tròn (O) có bán kính bằng 3 cm. Tính diện tích tam giác ABC.
Thảo luận (1)Hướng dẫn giải
Vì tam giác ABC đều nội tiếp đường tròn (O) nên O là trọng tâm, trực tâm của tam giác ABC.
Gọi H là giao điểm của AO và BC nên AH là trung trực đồng thời là đường cao, đường trung tuyến trong tam giác đều ABC.
Do đó: \(OA = \frac{{BC\sqrt 3 }}{3} \Rightarrow BC = \sqrt 3 OA = 3\sqrt 3 \left( {cm} \right)\)
Vì O là trọng tâm của tam giác ABC, AH là đường trung tuyến của tam giác ABC nên \(AH = \frac{3}{2}OA = \frac{3}{2}.3 = \frac{9}{2}\left( {cm} \right)\)
Diện tích tam giác ABC là:
\(S = \frac{1}{2}AH.BC = \frac{1}{2}.\frac{9}{2}.3\sqrt 3 = \frac{{27\sqrt 3 }}{4}\left( {c{m^2}} \right)\)
(Trả lời bởi datcoder)
Cho tam giác ABC nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC. Chứng minh rằng \(\widehat{BAH}=\widehat{OAC}\).
Thảo luận (1)Hướng dẫn giải
Ta có $O A=O B$ (cùng bằng bán kính đường tròn ngoại tiếp $(O)$ của $\triangle A B C$ ) nên $\triangle \mathrm{OAC}$ cân tại O , do đó $\widehat{O A C}=\widehat{O C A}$ (tính chất tam giác cân).
Lại có $\widehat{O A C}+\widehat{O C A}+\widehat{A O C}=180^{\circ}$ (tổng ba góc của một tam giác)
Suy ra $2 \widehat{O A C}+\widehat{A O C}=180^{\circ}$
Nên $\widehat{O A C}=\frac{180^{\circ}-\widehat{A O C}}{2}=90^{\circ}-\frac{\widehat{A O C}}{2}$.
Gọi K là giao điểm của AH và BC . Khi đó AK là đường cao của tam giac ABC .
Xét $\triangle A B K$ vuông tại K có: $\widehat{A B K}+\widehat{B A K}=90^{\circ}$ (tổng hai góc nhọn của tam giác vuông)Suy ra $\widehat{B A K}=90^{\circ}-\widehat{A B K}$ hay $\widehat{B A H}=90^{\circ}-\widehat{A B C}$. (2)
Mặt khác, xét đường tròn ( O ) có $\widehat{A B C}, \widehat{A O C}$ lần lượt là góc nội tiếp và góc ở tâm cùng chắn cung $A C$ nên $\widehat{A B C}=\frac{1}{2} \widehat{A O C}$. (3)Từ (2) và (3) ta có $\widehat{B A H}=90^{\circ}-\frac{\widehat{A O C}}{2}$.
(Trả lời bởi datcoder)
Từ (1) và (4) ta có $\widehat{B A H}=\widehat{O A C}$.
Cho đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F. Chứng minh rằng \(\widehat{EIF}+\widehat{BAC}=180^o\).
Thảo luận (1)Hướng dẫn giải
Vì đường tròn (I) nội tiếp tam giác ABC với các tiếp điểm trên các cạnh AB, AC lần lượt là E, F nên \(IF \bot AC,IE \bot AB \Rightarrow \widehat {IFA} = \widehat {AEI} = {90^o}\).
Tứ giác AEIF có:
\(\widehat {EAF} + \widehat {EIF} + \widehat {IFA} + \widehat {AEI} = {360^o}\)
\(\widehat {EIF} + \widehat {EAF} = {360^o} - \left( {\widehat {IFA} + \widehat {AEI}} \right) = {180^o} \)
Vậy \(\widehat {EIF} + \widehat {BAC} = {180^o}\).
(Trả lời bởi datcoder)
Cho tam giác đều ABC ngoại tiếp đường tròn (I). Tính độ dài các cạnh của tam giác ABC biết rằng bán kính của (I) bằng 1 cm..
Thảo luận (1)Hướng dẫn giải
Vì tam giác ABC ngoại tiếp đường tròn (I) và bán kính đường tròn (I) nội tiếp tam giác đều ABC bằng 1cm nên ta có: \(1 = \frac{{\sqrt 3 }}{6}BC \Rightarrow BC = 2\sqrt 3 \left( {cm} \right)\).
Vậy độ dài cạnh tam giác đều bằng \(2\sqrt 3 cm\).
(Trả lời bởi datcoder)
Người ta muốn làm một khung gỗ hình tam giác đều để đặt vừa khít một chiếc đồng hồ hình tròn có đường kính 30 cm (H.9.23). Hỏi độ dài các cạnh (phía bên trong) của khung gỗ phải bằng bao nhiêu?
Thảo luận (1)Hướng dẫn giải
Gọi khung gỗ hình tam giác đều là tam giác ABC.
Đồng hồ là đường tròn tâm I, bán kính \(IH = \frac{{30}}{2} = 15cm\)
Vì (I; IH) nội tiếp tam giác đều ABC nên \(IH = \frac{{\sqrt 3 }}{6}BC\), \(15 = \frac{{\sqrt 3 }}{6}BC\) nên \(BC = 30\sqrt 3 \left( {cm} \right)\)
Vậy độ dài cạnh khung gỗ phía bên trong bằng \(30\sqrt 3 cm\).
(Trả lời bởi datcoder)
