Trong đời sống hàng ngày, chúng ta thường gặp một số vật thể có dạng hình nón, như ở Hình 16.

Hình nón có những đặc điểm gì?
Trong đời sống hàng ngày, chúng ta thường gặp một số vật thể có dạng hình nón, như ở Hình 16.

Hình nón có những đặc điểm gì?
Cắt một miếng bìa có dạng tam giác vuông AOC. Khi quay miếng bìa một vòng quanh đường thẳng cố định chứa cạnh AO (Hình 17a), miếng bìa đó tạo nên một hình như ở Hình 17b. Hình đó có dạng hình gì?
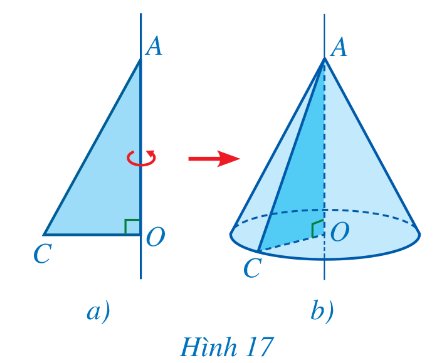
Thảo luận (1)Hướng dẫn giảiHình được tạo ra khi quay một tam giác vuông một vòng xung quanh đường thẳng cố định chứa một cạnh góc vuông của nó là hình nón.
(Trả lời bởi Nguyễn Quốc Đạt)
a) Cắt một miếng bìa có dạng hình tròn với bán kính 3 cm và tạo một đoạn dây mảnh không dãn có độ dài bằng chu vi của đường tròn bán kính 3 cm (Hình 19a).
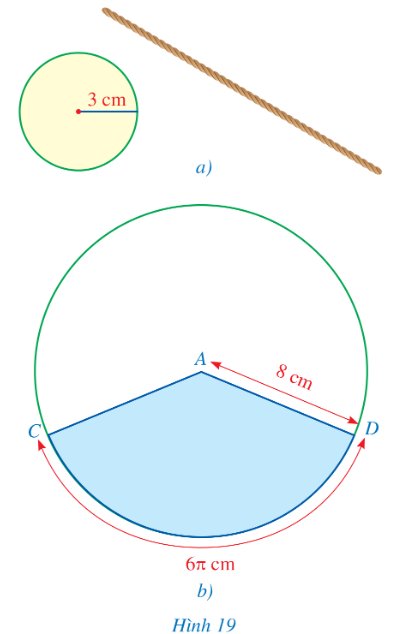
b) Lấy một miếng bìa có dạng hình tròn với bán kính bằng 8 cm; đánh dấu điểm C trên mép ngoài của hình tròn đó; gắn một đầu của đoạn dây ở Hình 19a vào điểm C rồi cuốn đoạn dây xung quanh hình tròn và đánh dấu đầu mút cuối của sợi dây là điểm D trên mép ngoài của hình tròn; cắt ra từ miếng bìa tròn đó hình quạt tròn CAD (Hình 19b).
c) Ghép và dán các miếng bìa vừa cắt ở câu a, b (Hình 20a) để được một hình nón như ở Hình 20b.
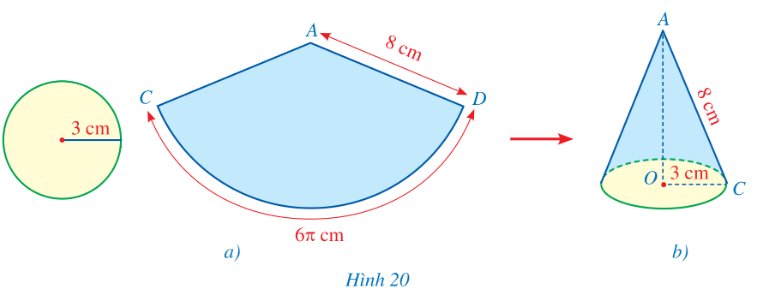
Thảo luận (1)Hướng dẫn giảiLàm theo hướng dẫn để cắt dán được hình nón như Hình 20b.
(Trả lời bởi Nguyễn Quốc Đạt)
Tạo lập một hình nón có bán kính đáy là 3 cm, chiều cao là 4 cm.
Thảo luận (1)Hướng dẫn giảiBước 1: Cắt một miếng bìa có dạng hình tròn với bán kính bằng 3cm và tạo một đoạn dây mảnh không dãn có độ dài bằng chu vi của đường tròn bán kính 3cm.
Bước 2: Đường sinh \(l = \sqrt {{3^2} + {4^2}} = 5cm.\) Lấy một miếng bìa có dạng hình tròn với bán kính bằng 5 cm; đánh dấu điểm trên mép ngoài của hình tròn đó; gắn một đầu của đoạn dây vào điểm đó rồi cuốn đoạn dây xung quanh hình tròn và đánh dấu đầu mút cuối của sợi dây trên mép ngoài của hình tròn; cắt ra từ miếng bìa tròn đó hình quạt tròn.
Bước 3: Ghép và dán các miếng bìa vừa cắt ở bước 1 và 2 để được một hình nón.
(Trả lời bởi Nguyễn Quốc Đạt)
Thực hiện các hoạt động sau:
a) Chuẩn bị một hình nón bằng giấy có bán kính đáy là r, chiều cao là h và độ dài đường sinh là l (Hình 21a);
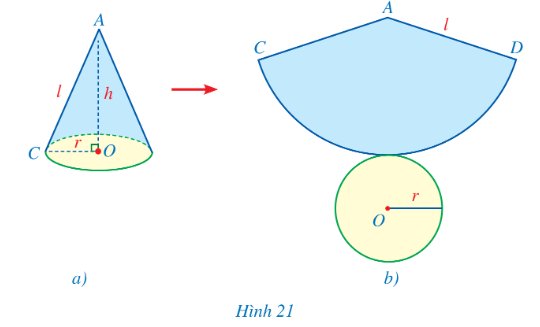
b) Từ hình nón đó, cắt rời đáy và cắt dọc theo đường sinh AC rồi trải phẳng ra, ta được hình khai triển mặt xung quanh của hình nón là một hình quạt tròn CAD tâm A với bán kính bằng độ dài đường sinh và độ dài cung CD bằng độ dài đường tròn đáy của hình nón (Hình 21b).
c) Tính diện tích hình quạt tròn CAD theo r và l.
Thảo luận (1)Hướng dẫn giảia) Cắt dán một hình nón tùy ý hoặc sử dụng hình có sẵn (mũ sinh nhật,…).
b) Làm theo hướng dẫn.
c) Diện tích quạt tròn CAD là:
\(\frac{1}{2}.C.l = \frac{1}{2}.2\pi r.l = \pi rl\) (C là chu vi đáy).
Vậy diện tích hình quạt tròn CAD là \(\pi rl\).
(Trả lời bởi Nguyễn Quốc Đạt)
Một chiếc nón lá có dạng hình nón với đường kính đáy khoảng 44 cm, chiều cao khoảng 20 cm. Hỏi diện tích xung quanh của chiếc nón đó bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?

Thảo luận (1)Hướng dẫn giải
Chiếc nón lá được biểu diễn dạng hình học như hình bên.
Bán kính đáy là:
\(44:2 = 22\left( {cm} \right)\)
Đường sinh là:
\(l = \sqrt {{r^2} + {h^2}} = \sqrt {{{22}^2} + {{20}^2}} = 2\sqrt {221} \left( {cm} \right)\) (áp dụng định lý Pytago cho tam giác vuông AOC).
Diện tích xung quanh của chiếc nón là:
\({S_{xq}} = \pi rl = 3,14.22.2\sqrt {221} \approx 2054\left( {c{m^2}} \right)\)
Vậy diện tích xung quanh của chiếc nón đó là khoảng \(2054c{m^2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai dụng cụ đựng nước: một dụng cụ có dạng hình nón và một dụng cụ có dạng hình trụ với chiều cao và bán kính đáy của hai dụng cụ bằng nhau (Hình 22a).
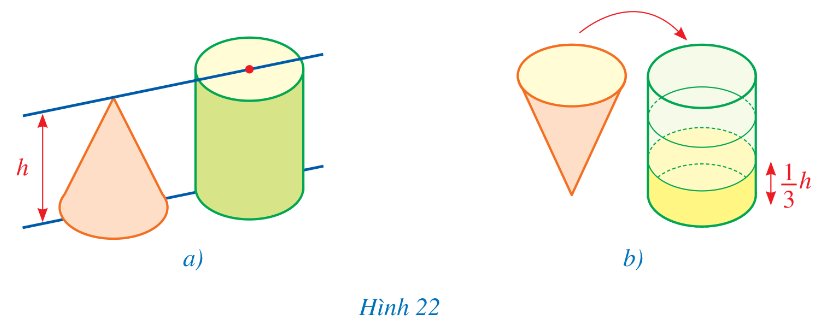
Đổ đầy nước vào dụng cụ có dạng hình nón rồi đổ nước từ dụng cụ đó sang dụng cụ có dạng hình trụ (Hình 22b). Ta cứ làm như thế ba lần và quan sát thấy dụng cụ có dạng hình trụ vừa đầy nước. Từ đó, hãy cho biết thể tích của dụng cụ có dạng hình trụ gấp bao nhiêu lần thể tích của dụng cụ có dạng hình nón.
Thảo luận (1)Hướng dẫn giảiThể tích của dụng cụ có dạng hình trụ gấp 3 lần thể tích của dụng cụ có dạng hình nón.
(Trả lời bởi Nguyễn Quốc Đạt)
Trong các hình 24a, 24b, 24c, hình nào có dạng hình nón (trong đó, O là tâm của mặt đáy, r là bán kính đáy, h là chiều cao)?
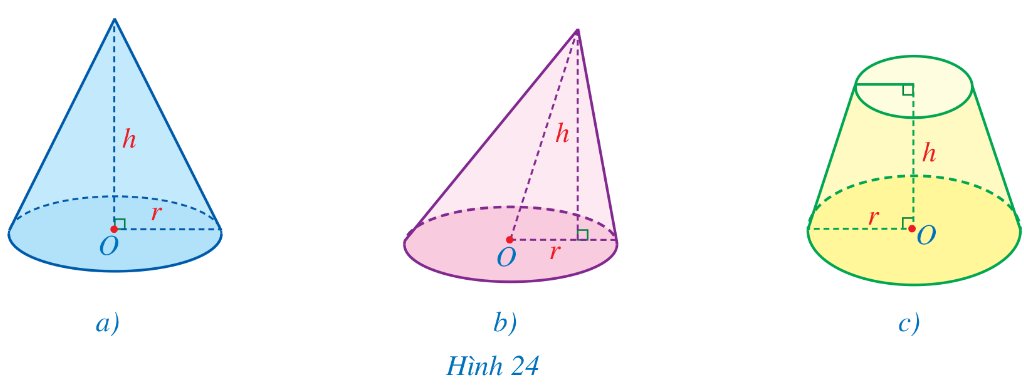
Thảo luận (2)Hướng dẫn giảihình a)
(Trả lời bởi Nguyễn Ngọc Thái)
Cho tam giác cân ACD có O là trung điểm cạnh đáy CD. Xét hình nón được tạo ra khi quay tam giác vuông AOC một vòng xung quanh đường thẳng cố định chứa cạnh AO của tam giác vuông đó (Hình 25).
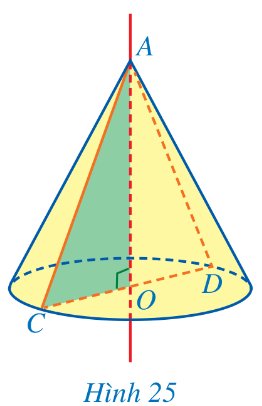
Quan sát Hình 25, hãy chỉ ra:
a) Đỉnh của hình nón;
b) Hai bán kính đáy của hình nón;
c) Chiều cao của hình nón;
d) Hai đường sinh của hình nón.
Thảo luận (1)Hướng dẫn giảia) Đỉnh của hình nón: A.
b) Hai bán kính đáy của hình nón: OC, OD.
c) Chiều cao của hình nón: OA.
d) Hai đường sinh của hình nón: AC, AD.
(Trả lời bởi Nguyễn Quốc Đạt)
Phần mái lá của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 m và độ dài đường sinh khoảng 8,5 m (Hình 26). Chi phí để làm phần mái lá đó là 250 000 đồng/1 m2 . Hỏi tổng chi phí để làm toàn bộ phần mái lá đó là bao nhiêu đồng?

Thảo luận (1)Hướng dẫn giảiPhần mái lá của một ngôi nhà được biểu diễn dạng hình nón.
Bán kính đáy là: \(12:2 = 6\left( m \right).\)
Diện tích xung quanh của mái lá là:
\({S_{xq}} = \pi rl = \pi .6.8,5 \approx 160,14\left( {{m^2}} \right).\)
Tổng chi phí để làm toàn bộ phần mái nhà đó là:
\(160,14.250000 = 40.035.000\)(đồng).
Vậy tổng chi phí để làm toàn bộ phần mái nhà đó là \(40.035.000\) đồng.
(Trả lời bởi Nguyễn Quốc Đạt)