Cho ABCD là hình bình hành. Đặt \(\overrightarrow {AB} = \overrightarrow a ,\overrightarrow {AD} = \overrightarrow b .\) Gọi G là trọng tâm của tam giác ABC. Biểu thị các vecto \(\overrightarrow {AG} ,\overrightarrow {CG} \) theo hai vecto \(\overrightarrow a ,\overrightarrow b .\)
$5. Tích của một số với một vectơ
Bài 6 (SGK Cánh Diều trang 92)
Thảo luận (2)
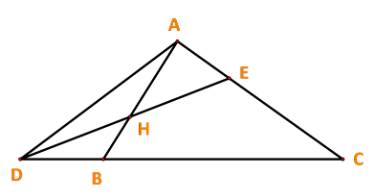
Bài 7 (SGK Cánh Diều trang 92)
Cho tam giác ABC. Các điểm D, E, H thỏa mãn
\(\overrightarrow {DB} = \frac{1}{3}\overrightarrow {BC} ,\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} ,\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .\)
a) Biểu thị mỗi vecto \(\overrightarrow {AD} ,\overrightarrow {DH} ,\overrightarrow {HE} \) theo hai vecto \(\overrightarrow {AB} ,\overrightarrow {AC} .\)
b) Chứng minh D, E, H thẳng hàng.
Thảo luận (1)Hướng dẫn giải
Dễ thấy: \(\overrightarrow {BC} = \overrightarrow {BA} + \overrightarrow {AC} = - \overrightarrow {AB} + \overrightarrow {AC} \)
Ta có:
+) \(\overrightarrow {AD} = \overrightarrow {AB} + \overrightarrow {BD} \). Mà \(\overrightarrow {BD} = - \overrightarrow {DB} = - \frac{1}{3}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AD} = \overrightarrow {AB} + \left( { - \frac{1}{3}} \right)( - \overrightarrow {AB} + \overrightarrow {AC} ) = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} \)
+) \(\overrightarrow {DH} = \overrightarrow {DA} + \overrightarrow {AH} = - \overrightarrow {AD} + \overrightarrow {AH} \).
Mà \(\overrightarrow {AD} = \frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} ;\;\;\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} .\)
\( \Rightarrow \overrightarrow {DH} = - \left( {\frac{4}{3}\overrightarrow {AB} - \frac{1}{3}\overrightarrow {AC} } \right) + \frac{2}{3}\overrightarrow {AB} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)
+) \(\overrightarrow {HE} = \overrightarrow {HA} + \overrightarrow {AE} = - \overrightarrow {AH} + \overrightarrow {AE} \)
Mà \(\overrightarrow {AH} = \frac{2}{3}\overrightarrow {AB} ;\;\overrightarrow {AE} = \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} .\)
b)
Theo câu a, ta có: \(\overrightarrow {DH} = \overrightarrow {HE} = - \frac{2}{3}\overrightarrow {AB} + \frac{1}{3}\overrightarrow {AC} \)
\( \Rightarrow \) Hai vecto \(\overrightarrow {DH} ,\overrightarrow {HE} \) cùng phương.
\( \Leftrightarrow \)D, E, H thẳng hàng
(Trả lời bởi Hà Quang Minh)