Tìm tâm và bán kính của đường tròn trong môi trường hợp sau:
a) Đường tròn có phương trình\({(x + 1)^2} + {(y - 5)^2} = 9\) ;
b) Đường tròn có phương trình\({x^2} + {y^2}-6x - 2y-{\rm{1}}5 = 0\) .
Tìm tâm và bán kính của đường tròn trong môi trường hợp sau:
a) Đường tròn có phương trình\({(x + 1)^2} + {(y - 5)^2} = 9\) ;
b) Đường tròn có phương trình\({x^2} + {y^2}-6x - 2y-{\rm{1}}5 = 0\) .
Lập phương trình đường tròn trong mỗi trường hợp sau:
a) Đường tròn có tâm I(- 3 ; 4) bán kính R = 9;
b) Đường tròn có tâm I(5 ;-2) và đi qua điểm M(4;- 1);
c) Đường tròn có tâm I(1;- 1) và có một tiếp tuyến là A: 5x- 12y – 1 = 0;
d) Đường tròn đường kính AB với A(3;-4) và B(-1; 6);
e) Đường tròn đi qua ba điểm A(1;1), B(3; 1), C(0; 4).
Thảo luận (1)Hướng dẫn giảia) Phương trình đường tròn là: \({\left( {x + 3} \right)^2} + {\left( {y - 4} \right)^2} = 81\)
b) Bán kính đường tròn là: \(R = IM = \sqrt {{{\left( {4 - 5} \right)}^2} + {{\left( { - 1 + 2} \right)}^2}} = \sqrt 2 \)
Phương trình đường tròn là: \({\left( {x - 5} \right)^2} + {\left( {y + 2} \right)^2} = 2\)
c) Bán kính đường tròn là: \(R = \frac{{\left| {5.1 - 12.\left( { - 1} \right) - 1} \right|}}{{\sqrt {{5^2} + {{\left( { - 12} \right)}^2}} }} = \frac{{16}}{{13}}\)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y + 1} \right)^2} = {\left( {\frac{{16}}{{13}}} \right)^2}\)
d) Gọi \(I\left( {a;b} \right)\) là trung điểm AB. Vậy tọa độ điểm I là: \(I\left( {1;1} \right)\)
Bán kính đường tròn là: \(R = IA = \sqrt {{{\left( {3 - 1} \right)}^2} + {{\left( { - 4 - 1} \right)}^2}} = \sqrt {29} \)
Phương trình đường tròn là: \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = 29\)
e) Giả sử tâm đường tròn là điểm \(I\left( {a;b} \right)\). Ta có: \(IA = IB = IC \Leftrightarrow I{A^2} = I{B^2} = I{C^2}\)
Vì \(I{A^2} = I{B^2},I{B^2} = I{C^2}\) nên: \(\left\{ \begin{array}{l}{\left( {1 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2}\\{\left( {3 - a} \right)^2} + {\left( {1 - b} \right)^2} = {\left( {0 - a} \right)^2} + {\left( {4 - b} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 2\\b = 3\end{array} \right.\) b
Vậy \(I\left( {2;3} \right)\) và \(R = IA = \sqrt {{{\left( { - 1} \right)}^2} + {{\left( { - 2} \right)}^2}} = \sqrt 5 \)
Vậy phương trình đường tròn đi qua 3 điểm A,B, C là: \({\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} = 5\)
(Trả lời bởi Hà Quang Minh)
Lập phương trình tiếp tuyến tại điểm có hoành độ bằng 3 thuộc đường tròn
\({\left( {x + 2} \right)^2} + {\left( {y + 7} \right)^2} = 169\).
Thảo luận (1)Hướng dẫn giảiTọa độ tiếp điểm là: \({M_1}\left( {3;5} \right),{M_2}\left( {3; - 12} \right)\)
Phương trình tiếp tuyến của đường tròn đi qua \({M_1}\) là: \( - 5\left( {x - 3} \right) - 12\left( {y - 5} \right) = 0 \Leftrightarrow - 5x - 12y + 75 = 0\)
Phương trình tiếp tuyến của đường tròn đi qua \({M_2}\) là:
\( - 5\left( {x - 3} \right) + 19(y + 12) = 0 \Leftrightarrow - 5x + 19y + 243 = 0\)
(Trả lời bởi Hà Quang Minh)
Tìm m sao cho đường thẳng 3x + 4y + m = 0 tiếp xúc với đường tròn
\({\left( {x + 1} \right)^2} + {\left( {y-2} \right)^2} = 4\).
Thảo luận (2)Hướng dẫn giảiĐể đường thẳng tiếp xúc với đường tròn thì \(d\left( {I,\Delta } \right) = R \Leftrightarrow \frac{{\left| {3.\left( { - 1} \right) + 4.2 + m} \right|}}{{\sqrt {{3^2} + {4^2}} }} = 2 \Leftrightarrow \left[ \begin{array}{l}m = 5\\m = - 15\end{array} \right.\)
(Trả lời bởi Hà Quang Minh)
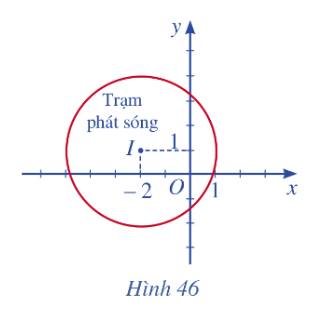
Hình 46 mô phỏng một trạm thu phát sóng điện thoại di động đặt ở vị trí 1 có toạ độ (- 2 ; 1) trong mặt phẳng toạ độ (đơn vị trên hai trục là ki-lô-mét).
a) Lập phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng, biết rằng trạm thu phát sóng đó được thiết kế với bán kính phủ sóng 3 km.
b) Nếu người dùng điện thoại ở vị trí có toạ độ (-1;3) thì có thể sử dụng dịch vụ của trạm này không? Giải thích.
c) Tính theo đường chim bay, xác định khoảng cách ngắn nhất để một người ở vị trí có toạ độ (-3;4) di chuyển được tới vùng phủ sóng theo đơn vị ki-lô-mét (làm tròn kết quả đến hàng phần mười).
Thảo luận (1)Hướng dẫn giảia) Phương trình đường tròn mô tả ranh giới bên ngoài của vùng phủ sóng là: \({\left( {x + 2} \right)^2} + {\left( {y - 1} \right)^2} = 9\)
b) Khoảng cách từ tâm I đến A là: \(IA = \sqrt {{{\left( { - 1 + 2} \right)}^2} + {{\left( {3 - 1} \right)}^2}} = \sqrt 5 \)
Do \(IA < 3\) nên điểm A nằm trong đường tròn ranh giới. Vậy nên người A có thể dịch vụ của trạm.
c) Khoảng cách từ tâm I đến B là: \(IB = \sqrt {{{\left( { - 3 + 2} \right)}^2} + {{\left( {4 - 1} \right)}^2}} = \sqrt {10} \)
Khoảng cách ngắn nhất theo đường chim bay để 1 người ở B di chuyển đến vùng phủ sóng là:
\(IB - R = \sqrt {10} - 3\left( {km} \right)\)
(Trả lời bởi Hà Quang Minh)
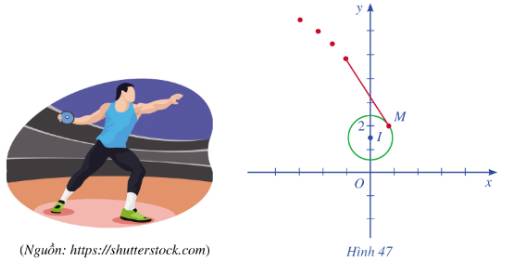
Ném đĩa là một môn thể thao thi đấu trong Thế vận hội Olympic mùa hè. Khi thực hiện cú ném, vận động viên thường quay lưng lại với hướng ném, sau đó xoay ngược chiều kim đồng hồ một vòng rưỡi của đường tròn để lấy đà rồi thả tay ra khỏi đĩa. Giả sử đĩa chuyển động trên một đường tròn tâm \(I\left( {0;\frac{3}{2}} \right)\) bán kính 0,8 trong mặt phẳng toạ độ Oxy (đơn vị trên hai trục là mét). Đến điểm\(M\left( {\frac{{\sqrt {39} }}{2};2} \right)\), đĩa được ném đi (Hình 47). Trong những giây đầu tiên ngay sau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa có phương trình như thế nào?
Thảo luận (2)Hướng dẫn giảiSau khi được ném đi, quỹ đạo chuyển động của chiếc đĩa nằm trên tiếp tuyến của đường tròn tâm I tại điểm M.
Vậy quỹ đạo chuyển động của chiếc đĩa nằm trên đường thẳng có phương trình là:
\(\begin{array}{l}\left( {\frac{{\sqrt {39} }}{{10}} - 0} \right)\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \left( {2 - \frac{3}{2}} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{{\sqrt {39} }}{{10}}\left( {x - \frac{{\sqrt {39} }}{{10}}} \right) + \frac{1}{2}\left( {y - 2} \right) = 0\\ \Leftrightarrow \sqrt {39} x + 5y - 13,9 = 0\end{array}\)
(Trả lời bởi Hà Quang Minh)