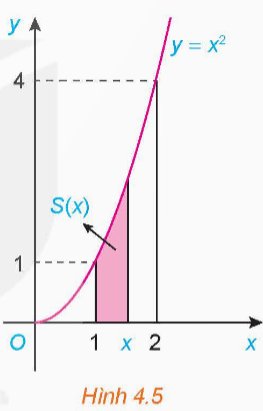
Xét hình thang cong giới hạn bởi đồ thị $y=x^2$, trục hoành và hai đường thẳng $x=1, x=2$. Ta muốn tính diện tích $S$ của hình thang cong này.
a) Với mỗi $x \in[1 ; 2]$, gọi $S(x)$ là diện tích phần hình thang cong đã cho nằm giữa hai đường thẳng vuông góc với trục $0 x$ tại điểm có hoành độ bằng 1 và $x(\mathrm{H} .4 .5)$.
Cho $h>0$ sao cho $x+h<2$. So sánh hiệu $S(x+h)-S(x)$ với diện tích hai hình chữ nhật MNPQ và MNEF (H.4.6). Từ đó suy ra $0 \leq \frac{S(x+h)-S(x)}{h}-x^2 \leq 2 x h+h^2$.
b) Cho $h<0$ sao cho $x+h>1$. Tương tự phần a, đánh giá hiệu $S(x)-S(x+h)$ và từ đó suy ra $2 x h+h^2 \leq \frac{S(x+h)-S(x)}{h}-x^2 \leq 0$.
c) Từ kết quả phần a và phần b, suy ra với mọi $\mathrm{h} \neq 0$, ta có $\left|\frac{S(x+h)-S(x)}{h}-x^2\right| \leq 2 x|h|+h^2$.
Từ đó chứng minh $S^{\prime}(x)=x^2, x \in(1 ; 2)$.
Người ta chứng minh được $S^{\prime}(1)=1, S^{\prime}(2)=4$, tức là $S(x)$ là một nguyên hàm của $x^2$ trên $[1 ; 2]$.
d) Từ kết quả của phần c , ta có $S(x)=\frac{x^3}{3}+C$. Sử dụng điều này với lưu ý $\mathrm{S}(1)=0$ và diện tích cần tính $\mathrm{S}=$ $S(2)$, hãy tính $S$.
Gọi $F(x)$ là một nguyên hàm tùy ý của $f(x)=x^2$ trên $[1 ; 2]$. Hãy so sánh $S$ và $F(2)-F(1)$.
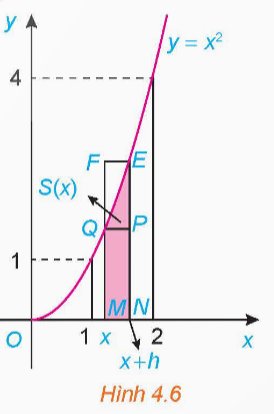
a) Với \(h > 0\) sao cho \(x + h < 2\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( {x + h} \right) - S\left( x \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = \left( {x + h - x} \right){x^2} = h{x^2}\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = \left( {x + h - x} \right){\left( {x + h} \right)^2} = h{\left( {x + h} \right)^2}\)
Do đó, \(h{x^2} \le S\left( {x + h} \right) - S\left( x \right) \le h{\left( {x + h} \right)^2}\). Vậy \(0 \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 2xh + {h^2}\)
b)
Với \(h < 0\) sao cho \(x + h > 1\), gọi \({S_{MNPQ}}\) và \({S_{MNEF}}\) lần lượt là diện tích các hình chữ nhật MNPQ và MNEF thì \({S_{MNPQ}} \le S\left( x \right) - S\left( {x + h} \right) \le {S_{MNEF}}\)
Diện tích hình chữ nhật MNPQ là: \({S_{MNPQ}} = MN.MQ = - h{\left( {x + h} \right)^2} > 0\)
Diện tích hình chữ nhật MNEF là: \({S_{MNEF}} = MN.NE = - h{x^2}\)
Do đó, \( - h{\left( {x + h} \right)^2} \le S\left( {x + h} \right) - S\left( x \right) \le - h{x^2}\)
Vậy \(2xh + {h^2} \le \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2} \le 0\) (do \(h < 0\) nên \( - h > 0\))
c) Từ phần a và phần b, suy ra với mọi \(h \ne 0\), ta có: \(\left| {\frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} - {x^2}} \right| \le 2x\left| h \right| + {h^2}\)
Do đó, \(S'\left( x \right) = \mathop {\lim }\limits_{h \to 0} \frac{{S\left( {x + h} \right) - S\left( x \right)}}{h} = {x^2},x \in \left( {1;2} \right)\). Suy ra, \(S'\left( 1 \right) = 1,S'\left( 2 \right) = 4\).
Do đó, S(x) là một nguyên hàm của \({x^2}\) trên \(\left[ {1;2} \right]\).
d) Theo c ta có: \(S\left( x \right) = \frac{{{x^3}}}{3} + C\), \(S\left( 1 \right) = 0\) nên \(\frac{1}{3} + C = 0 \Leftrightarrow C = \frac{{ - 1}}{3}\).
Do đó, \(S\left( x \right) = \frac{{{x^3}}}{3} - \frac{1}{3}\)
Diện tích cần tính là: \(S = S\left( 2 \right) = \frac{{{2^3}}}{3} - \frac{1}{3} = \frac{7}{3}\)
Vì F(x) là một nguyên hàm tùy ý của \(f\left( x \right) = {x^2}\) trên \(\left[ {1;2} \right]\) nên \(F\left( x \right) = \frac{{{x^3}}}{3} + C,C \in \mathbb{R}\)
Ta có: \(F\left( 2 \right) - F\left( 1 \right) = \frac{7}{3} - 0 = \frac{7}{3} = S\). Do đó, \(S = F\left( 2 \right) - F\left( 1 \right)\)


