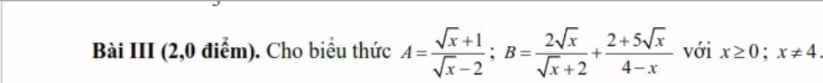Cách 1:
\(P=\frac{3\sqrt{x}\left(\sqrt{x}+2\right)+27}{\sqrt{x}+2}=3\sqrt{x}+\frac{27}{\sqrt{x}+2}=3\left(\sqrt{x}+2\right)+\frac{27}{\sqrt{x}+2}-6\)
\(P\ge2\sqrt{\frac{3\left(\sqrt{x}+2\right).27}{\sqrt{x}+2}}-6=12\)
\(P_{min}=12\) khi \(\sqrt{x}+2=\frac{9}{\sqrt{x}+2}\Leftrightarrow x=1\)
Cách 2:
\(P=\frac{12\left(\sqrt{x}+2\right)+3x-6\sqrt{x}+3}{\sqrt{x}+2}=12+\frac{3\left(\sqrt{x}-1\right)^2}{\sqrt{x}+2}\ge12\)
\(P_{min}=12\) khi \(x=1\)
Tìm giá trị nguyên của biểu thức \(A=\dfrac{\sqrt{x}}{6\sqrt{x}+1}\)
Giúp mình với ạ. Câu này không lấy tử chia mẫu được
Hỗ trợ em bài này ạ. Tìm GTLN và GTNN của biểu thức P=\(\dfrac{4\sqrt{x}}{3\left(x-\sqrt{x}+1\right)}\)
cho biểu thức R=\(\frac{\sqrt{x}-2}{\sqrt{x}+2}\) với x≥0. tìm GTNN của R
Mình bị lỗi đề cho mình hỏi lại bài này làm như nào ạ
\(\left(\sqrt{27}-3\sqrt{2}+2\sqrt{6}\right):3\sqrt{3}\)
cho biểu thức P=\(\left(1-\frac{\sqrt{x}}{1+\sqrt{x}}\right)\left(\frac{\sqrt{x}+3}{\sqrt{x}-2}+\frac{\sqrt{x}+2}{3-\sqrt{x}}+\frac{\sqrt{x}+2}{x-5\sqrt{x}+6}\right)\)
với x≥0; x≠4; x≠9
1, rút gọn P
2, tìm tất cả các giá trị nguyên của x để P<0
3, tìm GTNN của P
Ôn Tập Cơ Bản
1) Tìm điều kiện để các biểu thức sau có nghĩa:
a) \(\sqrt{11-2x}\)
b) \(\sqrt{9x-18}\)
c) \(\sqrt{\dfrac{3}{x^2}}\)
d) \(\sqrt{\dfrac{5}{x-7}}\)
2) Rút gọn:
a) \(\sqrt{16x^2}-2x^2\) với x \(\ge\) 0
b) \(\sqrt{9\left(x+5\right)^2}+2-3x\) với x
c) \(\sqrt{\left(x-5\right)^2}-4x\) với x < 5
Rút gọn biểu thức \(A=\sqrt[3]{\frac{x^3-3x+\left(x^2-1\right)\sqrt{x^2-4}}{2}}+\sqrt[3]{\frac{x^3-3x-\left(x^2-1\right)\sqrt{x^2-4}}{2}}\) với x ≥ 2
Bài 1. Tìm điều kiện để các biểu thức sau có nghĩa:
a. \(\sqrt{2+8x}\).
b. \(\sqrt{\dfrac{-1}{5}x+9}\)
c.\(\sqrt{11-7x}\)
Bài 2. Rút gọn các biểu thức sau:
a. \(\sqrt{48a}\) . \(\sqrt{3a}\) \(-2a\) với a \(\ge\) 0
b. \(\dfrac{1}{3}\sqrt{54}-3\sqrt{24}-\dfrac{\sqrt{66}}{\sqrt{11}}\)
Bài 3: Tìm x, biết:
a. \(\sqrt{\left(2x+3\right)^2}=3\)
b. \(\sqrt{4\left(x-2\right)}-4\sqrt{x-2}+\sqrt{9\left(x-2\right)}=4\)
Ctv giúp em làm câu này với.
Câu hỏi : Tìm giá trị nguyên lớn nhất của x để P có giá trị nguyên.
Biết rằng : P = \frac{3\sqrt{x}}{\sqrt{x}+2}
cho biểu thức P=\(\dfrac{2\sqrt{x}}{\sqrt{x}+3}+\dfrac{\sqrt{x}+1}{\sqrt{x}-3}+\dfrac{3-11\sqrt{x}}{9-x}\) với x\(\ge\)0; x\(\ne\)9
1.tìm ĐKXĐ và rút gọn P
2.tính P khi x=7+2\(\sqrt{3}\)
3.tìm x để P<1
