Bài 10: Đường thẳng song song với một đường thẳng cho trước
Các câu hỏi tương tự
Bài tập 1: Cho đường thẳng b. Gọi a và a là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h, (I) và (II) là các nửa mặt phẳng bờ b. Gọi P, P là điểm cách đường thẳng b một khoảng bằng h, trong đó có P thuộc nửa mặt phẳng (I), P thuộc nửa mặt phẳng (II). Chứng minh rằng P thuộc a, P thuộc a. Bài tập 2: Xét tam giác ABC có cạnh BC cố định, đường cao ứng với cạnh BC luôn bằng 2cm. Đỉnh A của các tam giác đó nằm trên đường nào? Giúp mình với ạ!!!!
Đọc tiếp
Bài tập 1: Cho đường thẳng b. Gọi a và a' là hai đường thẳng song song với đường thẳng b và cùng cách đường thẳng b một khoảng bằng h, (I) và (II) là các nửa mặt phẳng bờ b. Gọi P, P' là điểm cách đường thẳng b một khoảng bằng h, trong đó có P thuộc nửa mặt phẳng (I), P' thuộc nửa mặt phẳng (II). Chứng minh rằng P thuộc a, P' thuộc a'.
Bài tập 2: Xét tam giác ABC có cạnh BC cố định, đường cao ứng với cạnh BC luôn bằng 2cm. Đỉnh A của các tam giác đó nằm trên đường nào?
Giúp mình với ạ!!!!
Cho đoạn thẳng AB. Kẻ tia Ax bất kì, lấy các điểm C, D, E sao cho AC = CD = DE. Qua C và D kẻ các đường thẳng song song với EB. Chứng minh rằn đoạn thẳng AB bị chia thành 3 phần bằng nhau.
Bài 1 . cho đoạn thẳng AB .Kẻ tia Ax bất kì . Trên tia Ax lấy các điểm C,D,E,F sao cho AC = CD = DE =EF . Kẻ đoạn thẳng FB . Qua C, D,E kẻ CC’ , DD’ , EE’ song song với FB ( C’ ,D’ ,E’ thuộc đoạn thẳng AB )
a, chứng minh AC’ = C’D’= D’E’= E’B ( bằng hai cách khác nhau )
b, cho DD’= 3 cm . Tính CC’ , FB (bằng hai cách khác nhau)
1. Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C,D,E sao cho ACCDDE. Kể đoạn thẳng EB. Qua C,D kẻ các đường thẳng song song với EB cắt AB lần lượt tại C,D.Chứng minh : ÁCCDDB
2. Cho điểm A nằm ngoài đường thẳng d và cách d một khoảng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm thuộc tia đối của tia BA sao cho BCBA. Khi B di chuyển trên đường thẳng d thì C di chuyển trên đường nào?
MẤY ANH CHỊ GIÚP EM VỚI! CẢM ƠN CÁC ANH CHỊ NHIỀU NHIỀU!
Đọc tiếp
1. Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C,D,E sao cho AC=CD=DE. Kể đoạn thẳng EB. Qua C,D kẻ các đường thẳng song song với EB cắt AB lần lượt tại C',D'.Chứng minh : ÁC'=C'D'=D'B
2. Cho điểm A nằm ngoài đường thẳng d và cách d một khoảng 2cm. Lấy điểm B bất kì thuộc đường thẳng d. Gọi C là điểm thuộc tia đối của tia BA sao cho BC=BA. Khi B di chuyển trên đường thẳng d thì C di chuyển trên đường nào?
MẤY ANH CHỊ GIÚP EM VỚI! CẢM ƠN CÁC ANH CHỊ NHIỀU NHIỀU!![]()
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C,D,E sao cho AC = CD = DE. Kẻ đoạn thẳng EB. Qua C,D kẻ các đường thẳng song song với EB cắt AB lần lượt tại C' , D'. Chứng minh: AC' = C'D' = D'B.
* Vẽ hình rồi chứng minh giùm mình nha
Cho hình chữ nhật ABCD, 2 đường chéo AC và BD cắt nhau tại O. Lấy E là điểm bất kì thuộc OA. BE cắt AD tại M, Qua P kẻ đường thẳng song song với BM cắt BC tại N và cắt AC tại F.
a) Chứng minh: BMDN là hình bình hành b) Chứng minh: O là trung điểm EF...
Đọc tiếp
Cho hình chữ nhật ABCD, 2 đường chéo AC và BD cắt nhau tại O. Lấy E là điểm bất kì thuộc OA. BE cắt AD tại M, Qua P kẻ đường thẳng song song với BM cắt BC tại N và cắt AC tại F.
a) Chứng minh: BMDN là hình bình hành b) Chứng minh: O là trung điểm EF c) Qua E kẻ đường thẳng song song với BD cắt AD tại H, cắt CD tại I. Gọi O' là trung điểm IH. Chứng minh OO' song song DN d) Gọi K là điểm đối xứng với D qua O'. Chứng minh: K, M, B thẳng hàng
Bài 109: Cho đoạn thẳng AB và đường thẳng d song song với AB và C là điểm bất kì thuộc đường thẳng d. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB và G là giao điểm của AM, BN.
a) Chứng minh các điểm C, G, P thẳng hàng
b) Khi C di chuyển trên đường thẳng d thì điểm G di chuyển trên đường nào?
Bài 110: Cho tam giác ABC cân tại A và M là điểm bất kì thuộc cạnh BC. Gọi D, E lần lượt là chân các đường vuông góc hạ từ M tới AB, AC. Kẻ BH ⊥ AC (H ϵ AC) và kẻ MK ⊥ BH (K ϵ BH). Chứng mi...
Đọc tiếp
Bài 109: Cho đoạn thẳng AB và đường thẳng d song song với AB và C là điểm bất kì thuộc đường thẳng d. Gọi M, N, P lần lượt là trung điểm của các cạnh BC, AC, AB và G là giao điểm của AM, BN.
a) Chứng minh các điểm C, G, P thẳng hàng
b) Khi C di chuyển trên đường thẳng d thì điểm G di chuyển trên đường nào?
Bài 110: Cho tam giác ABC cân tại A và M là điểm bất kì thuộc cạnh BC. Gọi D, E lần lượt là chân các đường vuông góc hạ từ M tới AB, AC. Kẻ BH ⊥ AC (H ϵ AC) và kẻ MK ⊥ BH (K ϵ BH). Chứng minh: MD = BK và MD + ME = BH
Bài 111: Cho tam giác ABC cân tại A và M là điểm di chuyển trên cạnh BC. Chứng minh tổng khoảng cách từ M tới AB và AC luôn không đổi.
Các bạn giúp mk với, mai mình nộp rồi!!!
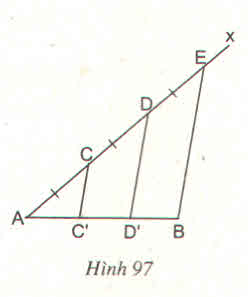
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC = CD = DE (h.97). Kẻ đoạn thẳng EB. Qua C, D kẻ các đường thẳng song song với EB. Chứng minh rằng đoạn thẳng AB bị chia ra thành 3 phần bằng nhau ?
Cho đoạn thẳng AB. Kẻ tia Ax bất kì. Trên tia Ax lấy các điểm C, D, E sao cho AC= CD = DE. Kẻ đoạn thẳng EB. QUa CC, D kể các đường thẳng song song với EB cắt AB lần lượt tại C' , D' . Chứng minh : AC" = C'D' = D'B
Giúp mình với, mai mình phải nộp bài tập rồi









