Tham khảo:
Bước 1:
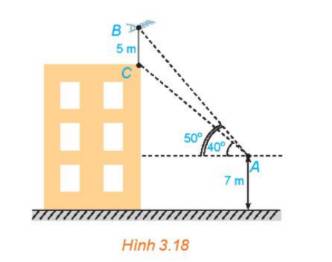
Đánh dấu vị trí quan sát tại điểm A, chiều rộng của hòn đảo kí hiệu là đoạn BC.
Gọi H là hình chiếu của A trên BC.
Trên tia đối của tia AH, lấy điểm M, ghi lại khoảng cách AM = a.
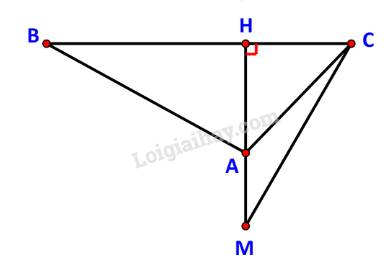
Bước 2:
Tại A, quan sát để xác định các góc \(\widehat {BAC} = \alpha ,\;\widehat {HAC} = \beta \).
Tiếp tục quan sát tại M, xác định góc \(\widehat {HMC} = \gamma \).
Bước 3: Giải tam giác AMC, tính AC.
AM = a, \(\widehat {AMC} = \widehat {HMC} = \gamma \) và \(\widehat {MAC} = {180^o} - \beta \)
\( \Rightarrow \widehat {ACM} = {180^o} - \gamma - \left( {{{180}^o} - \beta } \right) = \beta - \gamma \)
Áp dụng định định lí sin trong tam giác AMC ta có:
\(\frac{{AC}}{{\sin AMC}} = \frac{{AM}}{{\sin ACM}} \Rightarrow AC = \sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}\)
Bước 4:
\(\widehat {ABC} = {90^o} - \widehat {HAB} = {90^o} - (\alpha - \beta )\)
Áp dụng định lí sin cho tam giác ABC ta có:
\(\frac{{BC}}{{\sin A}} = \frac{{AC}}{{\sin B}} \Rightarrow BC = \sin \alpha .\frac{{\sin \gamma .\frac{a}{{\sin \left( {\beta - \gamma } \right)}}}}{{\sin \left( {{{90}^o} - (\alpha - \beta )} \right)}}.\).