Trong một nhà hàng, mỗi tuần để chế biến x phần ăn (x lấy giá trị trong khoảng từ 30 đến 120) thì chi phí trung bình (đơn vị: nghìn đồng) của một phần ăn được cho bởi công thức:
\(\overline{C}\left(x\right)=2x-230+\dfrac{7200}{x}\).
a) Khảo sát và vẽ đồ thị hàm số \(y=\overline{C}\left(x\right)\) trên [30; 120].
b) Từ kết quả trên, tìm số phần ăn sao cho chi phí trung bình của một phần ăn là thấp nhất.
Tập xác định: \(D = [30;120]\)
- Chiều biến thiên:
\(\overline C '(x) = 2 - \frac{{7200}}{{{x^2}}} = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 60(loai)\\x = 60\end{array} \right.\)
Trên các khoảng (30; 60) thì y' < 0 nên hàm số nghịch biến trên khoảng đó. Trên khoảng (60; 120) thì y' > 0 nên hàm số đồng biến trên khoảng đó.
- Cực trị:
Hàm số đạt cực đại tại x = 60 và \({y_{cd}} = 10\)
- Các giới hạn tại vô cực:
\(\mathop {\lim }\limits_{x \to - \infty } \overline C (x) = \mathop {\lim }\limits_{x \to - \infty } (2x - 230 + \frac{{7200}}{x}) = - \infty \); \(\mathop {\lim }\limits_{x \to + \infty } \overline C (x) = \mathop {\lim }\limits_{x \to + \infty } (2x - 230 + \frac{{7200}}{x}) = + \infty \)
- Bảng biến thiên:
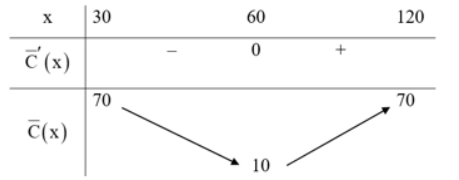
Đồ thị hàm số:
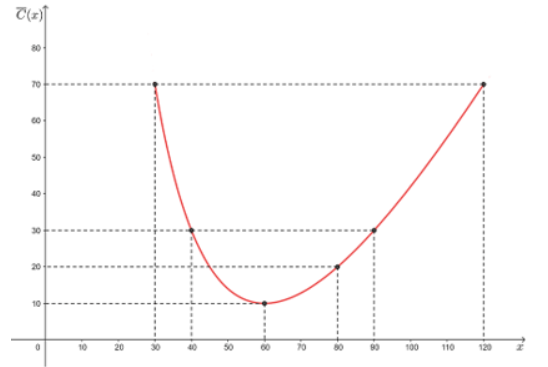
b) Từ bảng biến thiên, ta thấy \(\mathop {\min }\limits_{[30;120]} \overline C (x) = \overline C (60) = 10\)
Vậy để chi phí trung bình của một phần ăn là thấp nhất thì số phần ăn là 10


