Tham khảo:
a) Ta có: \(\overrightarrow {OA} = \left( {2;1} \right)\) ( do A(2; 1)) và \(\overrightarrow {OB} = \left( {3;3} \right)\) (do B (3; 3)).
Hai vectơ này không cùng phương (vì \(\frac{2}{3} \ne \frac{1}{3}\)).
Do đó các điểm O, A, B không cùng nằm trên một đường thẳng.
Vậy chúng không thẳng hàng.
b) Các điểm O, A, B không thẳng hàng nên OABM là một hình hành khi và chỉ khi \(\overrightarrow {OA} = \overrightarrow {MB} \).
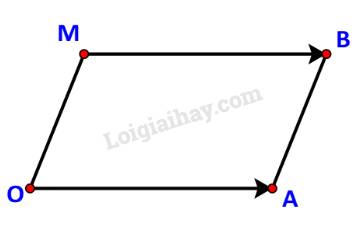
Do \(\overrightarrow {OA} = \left( {2;1} \right),\quad \overrightarrow {MB} = \left( {3 - x;3 - y} \right)\) nên
\(\overrightarrow {OA} = \overrightarrow {MB} \Leftrightarrow \left\{ \begin{array}{l}2 = 3 - x\\1 = 3 - y\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\\y = 2\end{array} \right.\)
Vậy điểm cần tìm là M (1; 2).