Tham khảo:
Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD
Tham khảo:

Tồn tại một và chỉ 1 mặt phẳng chứa hai đường thẳng AD và BD
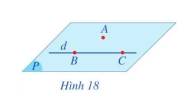
Cho điểm A không thuộc đường thẳng d. Lấy hai điểm phân biệt B và C thuộc đường thẳng d (Hình 18).
a) Mặt phẳng đi qua ba điểm A, B, C có đi qua đường thẳng d hay không?
b) Có bao nhiêu mặt phẳng đi qua điểm A và đường thẳng d?
Cho hình chóp tứ giác S.ABCD có đáy không là hình thang. Gọi M là trung điểm của SA.
a) Xác định giao điểm của CD với hai mặt phẳng (SAB) và (SCD)
b) Xác định giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Xác định giao tuyến của hai mặt phẳng (MCD) và (SBC)
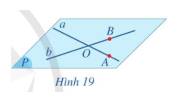
Cho hai đường thẳng a và b cắt nhau tại O. Lấy điểm A trên đường thẳng a (A khác O), lấy điểm B trên đường thẳng b (B khác O) (Hình 19).
a) Mặt phẳng đi qua ba điểm A, B, O có đi qua hai đường thẳng a và b hay không?
b) Có bao nhiêu mặt phẳng đi qua hai đường thẳng a và b?
Cho hình chóp S.ABCD có đáy là hình bình hành. Gọi M, N lần lượt là trung điểm của các cạnh SA và AD.
a) Xác định giao điểm của mặt phẳng (CMN) với các đường thẳng AB, SB
b) Xác định giao tuyến của mặt phẳng (CMN) với mỗi mặt phẳng (SAB) và (SBC)
Cho hình chóp S.ABC. Các điểm M, N lần lượt thuộc các cạnh SA, SC sao cho \(MA = 2MS,NS = 2NC\)
a) Xác định giao điểm của MN với mặt phẳng (ABC)
b) Xác định giao tuyến của mặt phẳng (BMN) với mặt phẳng (ABC)
Cho ba đường thẳng a, b, c không cùng nằm trong một mặt phẳng và đôi một cắt nhau. Chứng minh rằng ba đường thẳng a, b, c cùng đi qua một điểm, hay còn gọi là ba đường thẳng đồng quy.
Quan sát Hình 1, nếu coi mặt sân Napoleon là một phần của mặt phẳng (P) thì đỉnh của kim tự tháp có thuộc mặt phẳng (P) hay không?
Hình 25 là hình nhr của khối rubik tam giác (Pyramix). Quan sát Hình 25 và trả lời các câu hỏi:
a) Khối rubik tam giác có bao nhiêu đỉnh? Các đỉnh có cùng nằm trong một mặt phẳng không?
b) Khối rubik tam giác có bao nhiêu mặt? Mỗi mặt của khối rubik tam giác là những hình gì?

Trong Ví dụ 4, xác định giao tuyến của hai mặt phẳng (SAC) và (SBD).