Trong không gian với hệ trục tọa độ Oxyz, cho vectơ \(\overrightarrow{u}=\left(a;b;c\right)\) (Hình 31). Lấy điểm A sao cho \(\overrightarrow{OA}=\overrightarrow{u}\).
a) Tìm hoành độ, tung độ và cao độ của điểm A.
b) Biểu diễn vectơ \(\overrightarrow{OH}\) qua vectơ \(\overrightarrow{i}\), vectơ \(\overrightarrow{OK}\) qua vectơ \(\overrightarrow{j}\); vectơ \(\overrightarrow{OP}\) qua vectơ \(\overrightarrow{k}\).
c) Biểu diễn vectơ \(\overrightarrow{u}\) theo các vectơ \(\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}\).
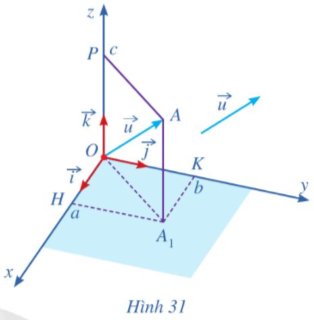
a) a là hoành độ của điểm A, b là tung độ của điểm A, c là cao độ của điểm A.
b) \(\overrightarrow {OH} = a\overrightarrow {i} \), \(\overrightarrow {OK} = b\overrightarrow {j} \), \(\overrightarrow {OP} = c\overrightarrow {k} \).
c) Áp dụng quy tắc hình hộp ta được: \(\vec u = a\overrightarrow {i} + b\overrightarrow {j} + c\overrightarrow {k}\).


