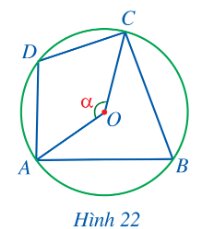
a) Xét (O) có \(\widehat {AOC}\) là góc ở tâm chắn cung CDA nên \(\widehat {AOC}\)= sđ\(\overset\frown{CDA}= \alpha.\)
\(\widehat {ABC}\) là góc nội tiếp chắn cung CDA của (O) nên \(\widehat {ABC}\)= \(\frac{1}{2}\)sđ\(\overset\frown{CDA}=\frac{ \alpha}{2}.\)
b) Xét (O) có sđ\(\overset\frown{ABC}=360{}^\circ -\)sđ\(\overset\frown{CDA}=360{}^\circ - \alpha.\)
\(\widehat {ADC}\) là góc nội tiếp chắn cung ABC của (O) nên\(\widehat {ADC}\) = \(\frac{1}{2}\)sđ\(\overset\frown{ABC}=\frac{360{}^\circ - \alpha}{2}.\)
c) \(\widehat {ADC} + \widehat {ABC} = \frac{{360^\circ - \alpha}}{2} + \frac{ \alpha}{2} = \frac{{360^\circ - \alpha + \alpha}}{2} = 180^\circ .\)