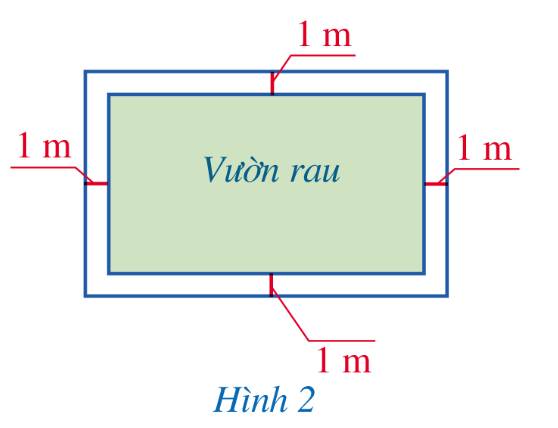
Nửa chu vi của mảnh đất là: \(52:2 = 26\left( m \right)\)
Gọi chiều dài của mảnh đất là \(x\left( {m,2 < x < 26} \right)\).
Chiều rộng của mảnh đất là: \(26 - x\,\left( m \right)\)
Chiều dài của vườn rau là: \(x - 2\,\,\left( m \right)\)
Chiều rộng của vườn rau là: \(26 - x - 2 = 24 - x\,\,\left( m \right)\)
Do diện tích của vườn rau là \(112{m^2}\) nên ta có phương trình:
\(\left( {x - 2} \right)\left( {24 - x} \right) = 112\)
\(24x - {x^2} - 48 + 2x - 112 = 0\)
\( - {x^2} + 26x - 160 = 0\)
\({x^2} - 26x + 160 = 0\)
\({\left( {x - 13} \right)^2} - 9 = 0\)
\(\left( {x - 13 - 3} \right)\left( {x - 13 + 3} \right) = 0\)
\(\left( {x - 16} \right)\left( {x - 10} \right) = 0\).
Để giải phương trình trên, ta giải hai phương trình sau:
*) \(x - 16 = 0\)
\(x = 16\);
*) \(x - 10 = 0\)
\(x = 10\).
Vậy chiều dài của mảnh đất là \(16\left( m \right)\)
Chiều rộng của mảnh đất là \(10\left( m \right)\)