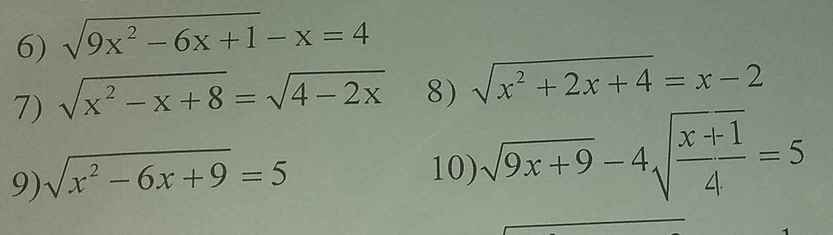1)b) \(B=\left(\sqrt{3+\sqrt{2}}-\sqrt{3}\right)\left(\sqrt{3+\sqrt{2}}+\sqrt{3}\right)\left(\sqrt{2-\sqrt{3}}\right)\)
\(B=\left[\left(\sqrt{3+\sqrt{2}}\right)^2-\sqrt{3}^2\right]\left(\sqrt{\dfrac{4-2\sqrt{3}}{2}}\right)\)
\(B=\left[3+\sqrt{2}-3\right]\left[\dfrac{\sqrt{\left(\sqrt{3}-1\right)^2}}{\sqrt{2}}\right]\)
\(B=\sqrt{2}\left(\dfrac{\sqrt{3}-1}{\sqrt{2}}\right)=\sqrt{3}-1\)
Đúng 0
Bình luận (2)
Giúp mình câu 7,9, mình cảm ơn.
