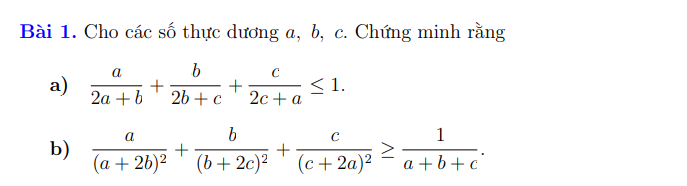Bài 5:
a) Ta có: \(A=\left(\dfrac{4x+5\sqrt{x}-1}{x\sqrt{x}+2x-\sqrt{x}-2}-\dfrac{3\sqrt{x}+1}{x+\sqrt{x}-2}\right):\dfrac{x+4\sqrt{x}+4}{x-1}\)
\(=\left(\dfrac{4x+5\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{\left(3\sqrt{x}+1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\left(\sqrt{x}+2\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{4x+5\sqrt{x}-1-3x-3\sqrt{x}-\sqrt{x}-1}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+2\right)^2}\)
\(=\dfrac{x+\sqrt{x}-2}{\left(\sqrt{x}+2\right)^3}\)
\(=\dfrac{\sqrt{x}-1}{x+4\sqrt{x}+4}\)
b) Ta có: \(A-1=\dfrac{\sqrt{x}-1-x-4\sqrt{x}-4}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+3\sqrt{x}+5\right)}{x+4\sqrt{x}+4}\)
\(=\dfrac{-\left(x+2\cdot\sqrt{x}\cdot\dfrac{3}{2}+\dfrac{9}{4}\right)-\dfrac{11}{4}}{x+4\sqrt{x}+4}< 0\forall x\) thỏa mãn ĐKXĐ
nên A<1











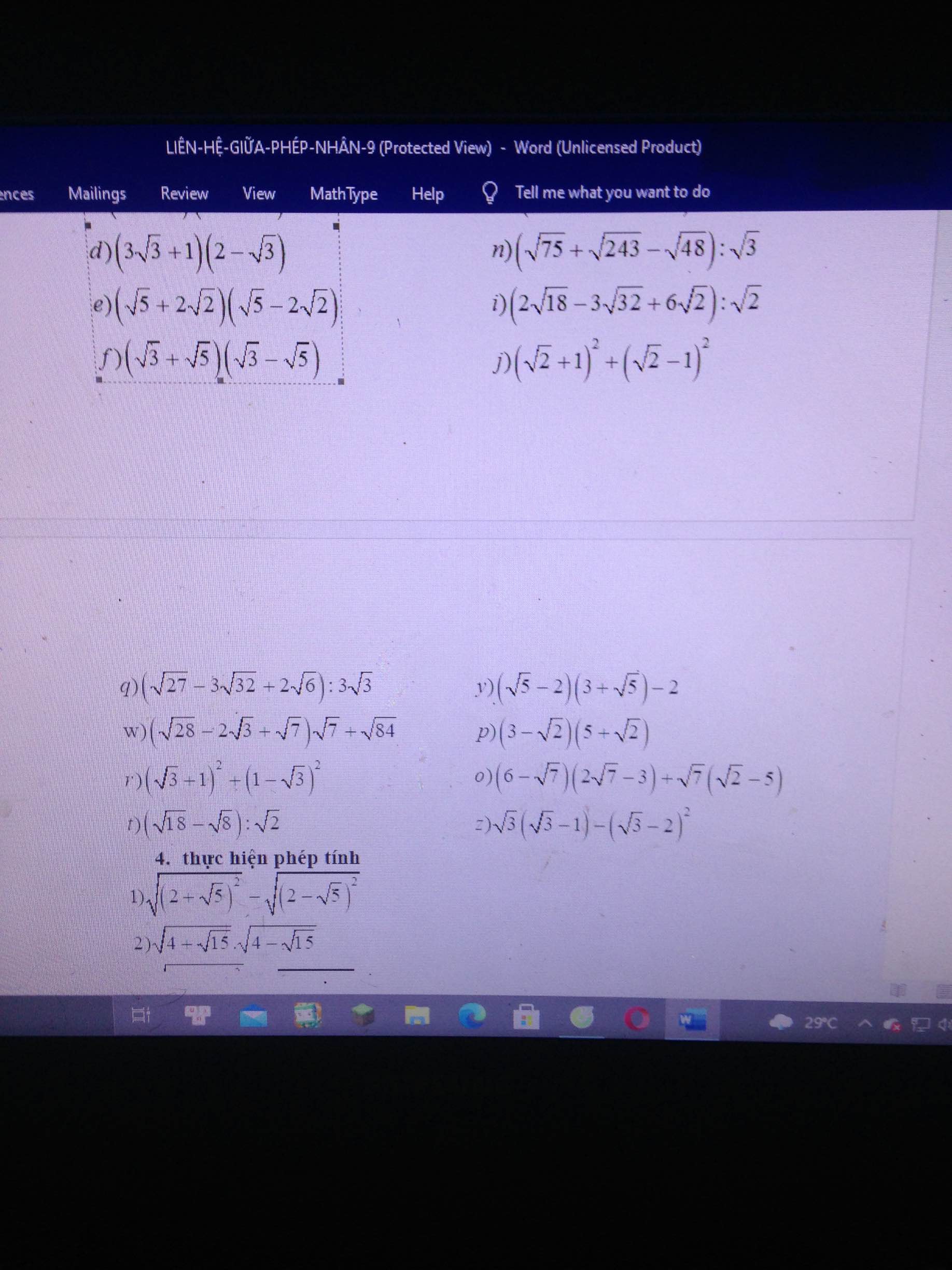



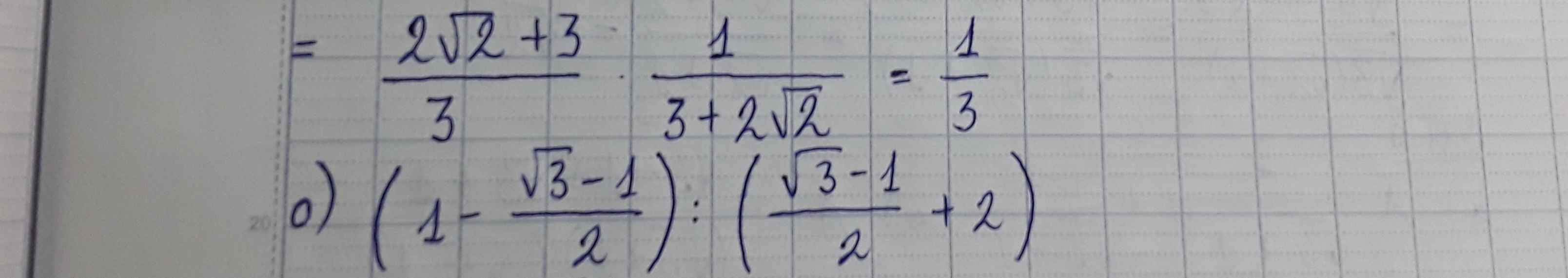 giải giúp mk câu o vs ạ
giải giúp mk câu o vs ạ