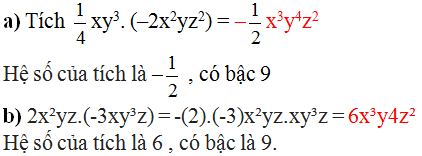a) Tích của và là:
Đơn thức tích có hệ số là ; có bậc 9.
b) Tích của và là:
Đơn thức có hệ số là 6; có bậc 9.
a) \(\dfrac{1}{4}xy^3.\left(-2\right)x^2yz^2\)
= \(\left[\dfrac{1}{4}.\left(-2\right)\right].\left(x.x^2\right).\left(y^3.y\right).z^2\)
= \(\dfrac{-1}{2}x^3y^4z^2\).
Đơn thức trên có hệ số là \(\dfrac{-1}{2}\) và bậc là 9.
b) \(-2x^2yz.\left(-3\right)xy^3z\)
= \(\left[\left(-2\right).\left(-3\right)\right].\left(x^2.x\right).\left(y.y^3\right).\left(z.z\right)\)
= 6x\(^3y^4z^2\).
Đơn thức trên có hệ số là 6 và bậc là 9.
a) Ta có: 1/4xy³.(-2x²yz²) = 1/2(-2)xy³.x²yz² = -1/2x³y4z²
– Hệ số của tích là -1/2 và tích có bậc là 9.
b)Ta có: 2x²yz.(-3xy³z) = -(2).(-3)x²yz.xy³z = 6x³y4z²
Hệ số của tích là 6 và tích có bậc là 9.
a) \(\dfrac{1}{4}xy^3.\left(-2\right)x^2yz^2\)
= \(\left[\dfrac{1}{4}.\left(-2\right)\right].\left(x.x^2\right).\left(y^3.y\right).z^2\)
= \(\dfrac{-1}{2}\)x\(^2\)\(y^4\)z\(^2\).
Hệ số là \(\dfrac{-1}{2}\); đơn thức trên bậc 8.
b) \(-2x^2yz.\left(-3\right)xy^3z\)
= \(\left[\left(-2\right).\left(-3\right)\right].\left(x^2.x\right).\left(y.y^3\right).\left(z.z\right)\)
= 6x\(^3y^4z^2\).
Hệ số là 6; đơn thức trên bậc 9.
a)Tích của \(\dfrac{1}{4}xy^3\)và -2x2yz2 là:
\(\dfrac{1}{4}xy^3\). ( -2x2yz2 ) = \(\dfrac{-1}{2}\)x3y4z2
Đơn thức trên có hệ số là \(\dfrac{-1}{2}\)và có bậc là 9
b)Tích của -2x2yz và-3xy3z là:
-2x2yz . (-3xy3z) = 6 x3y4z2
Đơn thức trên có hệ số là 6 và có bậc là 9
a)\(\dfrac{1}{4}xy^3\cdot\left(-2\right)x^2yz^2\)
=\(\dfrac{-1}{2}x^3y^4z^2\)
Hệ số:\(\dfrac{-1}{2}\)
Bậc:9
b) \(-2x^2yz\cdot\left(-3\right)xy^3z\)
=\(6x^3y^4z^2\)
Hệ số:6
Bậc:9
a) \(\dfrac{1}{4}xy^3\cdot\left(-2\right)x^2yz^2\)
=\(\dfrac{-1}{2}x^3y^4z^2\)
Hệ số:\(\dfrac{-1}{2}\)
Bậc:9
b) \(-2x^2yz\cdot\left(-3\right)xy^3z\)
=\(6x^3y^4z^2\)
Hệ số:6
Bậc:9